Union Find Exercise 1
Part 1. 基本概念
- 并查集是一种数据结构
- 并查集这三个字,一个字代表一个意思。
- 并(Union),代表合并
- 查(Find),代表查找
- 集(Set),代表这是一个以字典为基础的数据结构,它的基本功能是合并集合中的元素,查找集合中的元素
- 并查集的典型应用是有关连通分量的问题
- 并查集解决单个问题(添加,合并,查找)的时间复杂度都是O(1)
- 因此,并查集可以应用到在线算法中
Part 2. Union Find的实现
- 数据结构
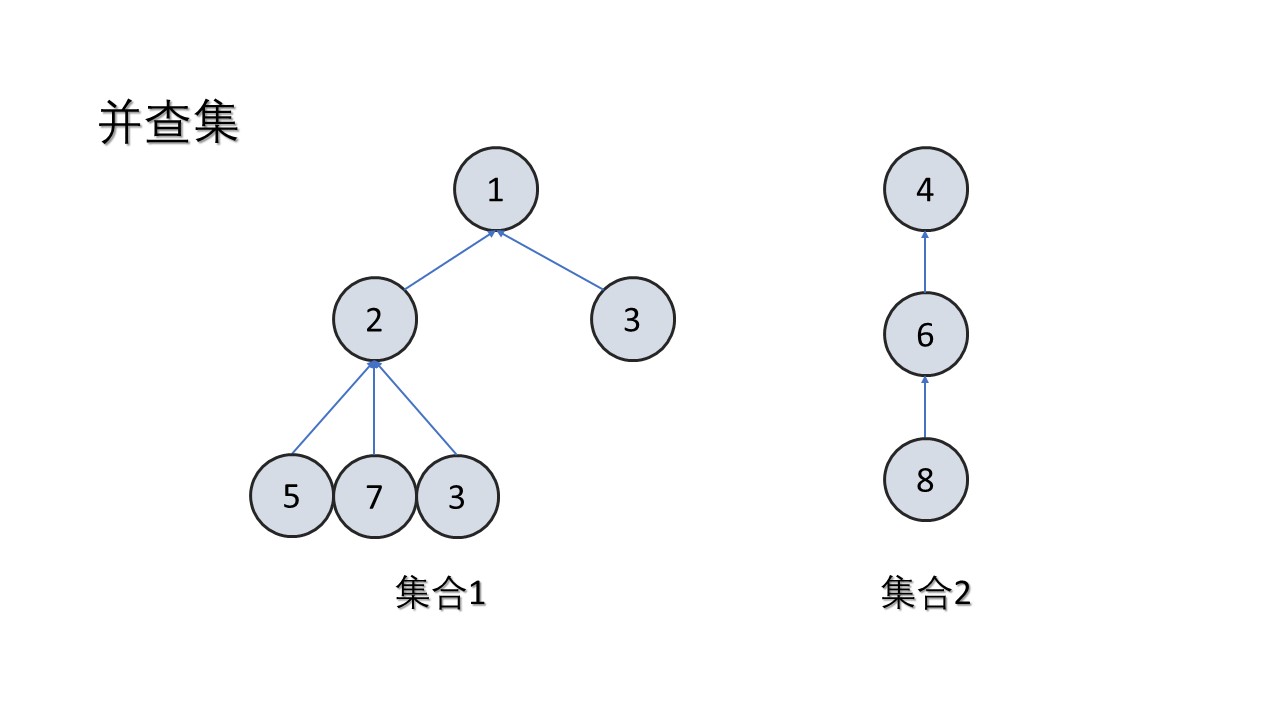
- 并查集跟树有些类似,只不过她跟树是相反的。在树这个数据结构里面,每个节点会记录它的子节点。在并查集里,每个节点会记录它的父节

- 如果节点是相互连通的(从一个节点可以到达另一个节点),那么他们在同一棵树里,或者说在同一个集合里,或者说他们的祖先是相同的。
- 初始化:
- 当把一个新节点添加到并查集中,它的父节点应该为空

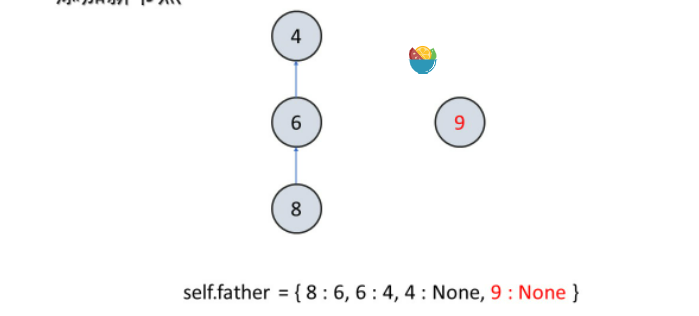
- 当把一个新节点添加到并查集中,它的父节点应该为空
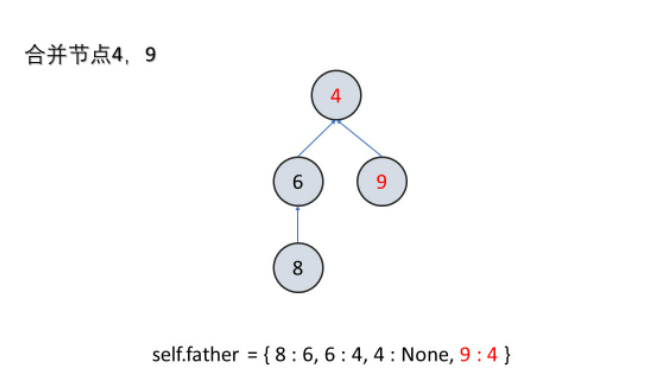
- 合并节点:
- 如果发现两个节点是连通的,那么就要把他们合并,也就是他们的祖先是相同的。这里究竟把谁当做父节点一般是没有区别的。

- 两节点是否连通
- 我们判断两个节点是否处于同一个连通分量的时候,就需要判断它们的祖先是否相同

- 查找祖先
- 查找祖先的方法是:如果节点的父节点不为空,那就不断迭代

- 这里有一个优化的点:如果我们树很深,比如说退化成链表,那么每次查询的效率都会非常低。所以我们要做一下路径压缩。也就是把树的深度固定为二。这么做可行的原因是,并查集只是记录了节点之间的连通关系,而节点相互连通只需要有一个相同的祖先就可以了。
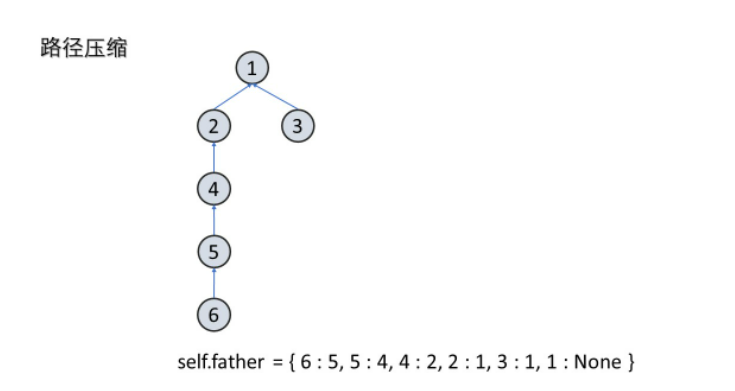
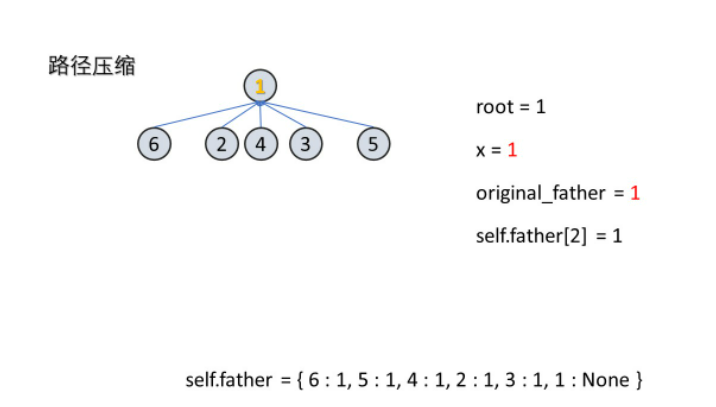


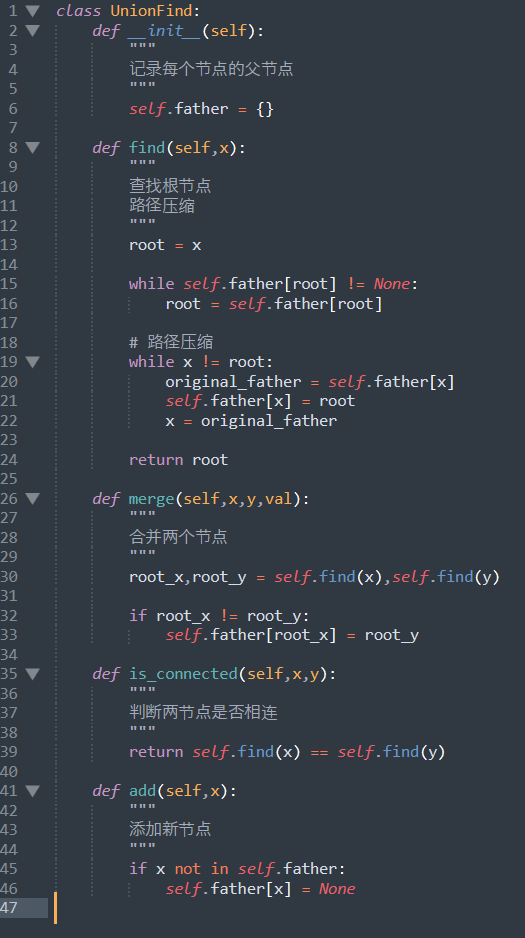
- 完整模板
上述的模板是无权的,加上权重以后,在原模板上添加几行即可。
990. Satisfiability of Equality Equations
难度中等230
You are given an array of strings equations that represent relationships between variables where each string equations[i] is of length 4 and takes one of two different forms: "xi==yi" or "xi!=yi".Here, xi and yi are lowercase letters (not necessarily different) that represent one-letter variable names.
Return true if it is possible to assign integers to variable names so as to satisfy all the given equations, or false otherwise.
Example 1:
Input: equations = ["a==b","b!=a"]
Output: false
Explanation: If we assign say, a = 1 and b = 1, then the first equation is satisfied, but not the second.
There is no way to assign the variables to satisfy both equations.
Example 2:
Input: equations = ["b==a","a==b"]
Output: true
Explanation: We could assign a = 1 and b = 1 to satisfy both equations.
Constraints:
1 <= equations.length <= 500equations[i].length == 4equations[i][0]is a lowercase letter.equations[i][1]is either'='or'!'.equations[i][2]is'='.equations[i][3]is a lowercase letter.
思路:
-
并查集分为两部分:
- 合并 两棵树合并,即:把【其中一颗树的根节点】的【父节点】,置为【另一颗树的根节点】
- 查询 根节点:父节点是它的本身 其他:递归查询它的父节点
-
主函数
- 构建包含所有相等元素的图 针对包含【!=】的式子,查询两端的字母是否包含在同一个集合中(即:根节点相同)
代码:
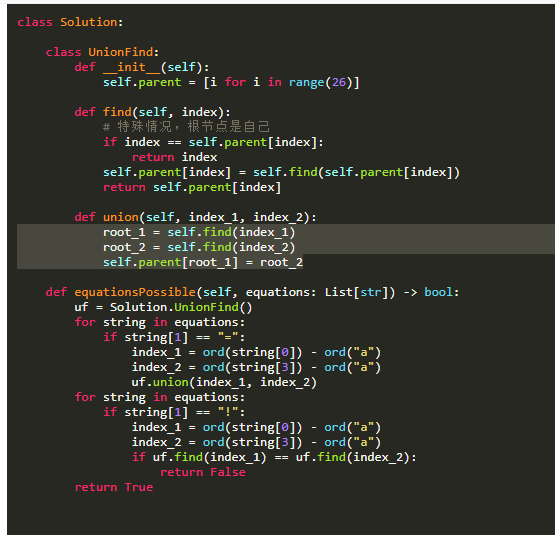
399. Evaluate Division
难度中等727
You are given an array of variable pairs equations and an array of real numbers values, where equations[i] = [Ai, Bi] and values[i] represent the equation Ai / Bi = values[i]. Each Ai or Bi is a string that represents a single variable.
You are also given some queries, where queries[j] = [Cj, Dj] represents the jth query where you must find the answer for Cj / Dj = ?.
Return the answers to all queries. If a single answer cannot be determined, return -1.0.
Note: The input is always valid. You may assume that evaluating the queries will not result in division by zero and that there is no contradiction.
Example 1:
Input: equations = [["a","b"],["b","c"]], values = [2.0,3.0], queries = [["a","c"],["b","a"],["a","e"],["a","a"],["x","x"]]
Output: [6.00000,0.50000,-1.00000,1.00000,-1.00000]
Explanation:
Given: a / b = 2.0, b / c = 3.0
queries are: a / c = ?, b / a = ?, a / e = ?, a / a = ?, x / x = ?
return: [6.0, 0.5, -1.0, 1.0, -1.0 ]
Example 2:
Input: equations = [["a","b"],["b","c"],["bc","cd"]], values = [1.5,2.5,5.0], queries = [["a","c"],["c","b"],["bc","cd"],["cd","bc"]]
Output: [3.75000,0.40000,5.00000,0.20000]
Example 3:
Input: equations = [["a","b"]], values = [0.5], queries = [["a","b"],["b","a"],["a","c"],["x","y"]]
Output: [0.50000,2.00000,-1.00000,-1.00000]
Constraints:
1 <= equations.length <= 20equations[i].length == 21 <= Ai.length, Bi.length <= 5values.length == equations.length0.0 < values[i] <= 20.01 <= queries.length <= 20queries[i].length == 21 <= Cj.length, Dj.length <= 5Ai, Bi, Cj, Djconsist of lower case English letters and digits.
思路:
-
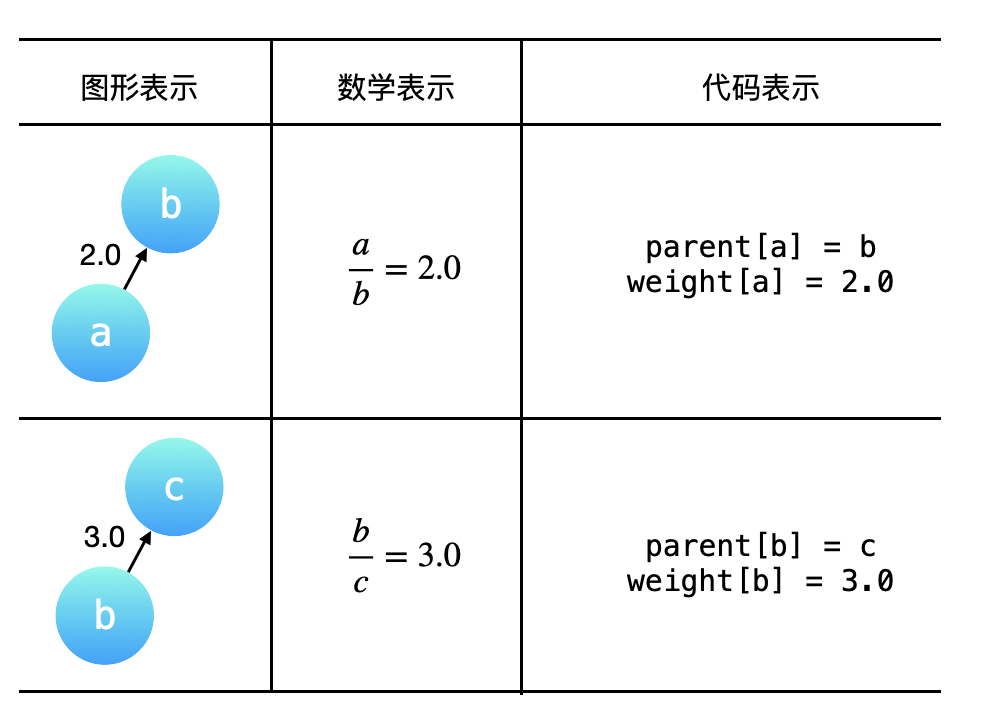
-
如何在「find查询」操作的「路径压缩」优化中维护权值变化
-
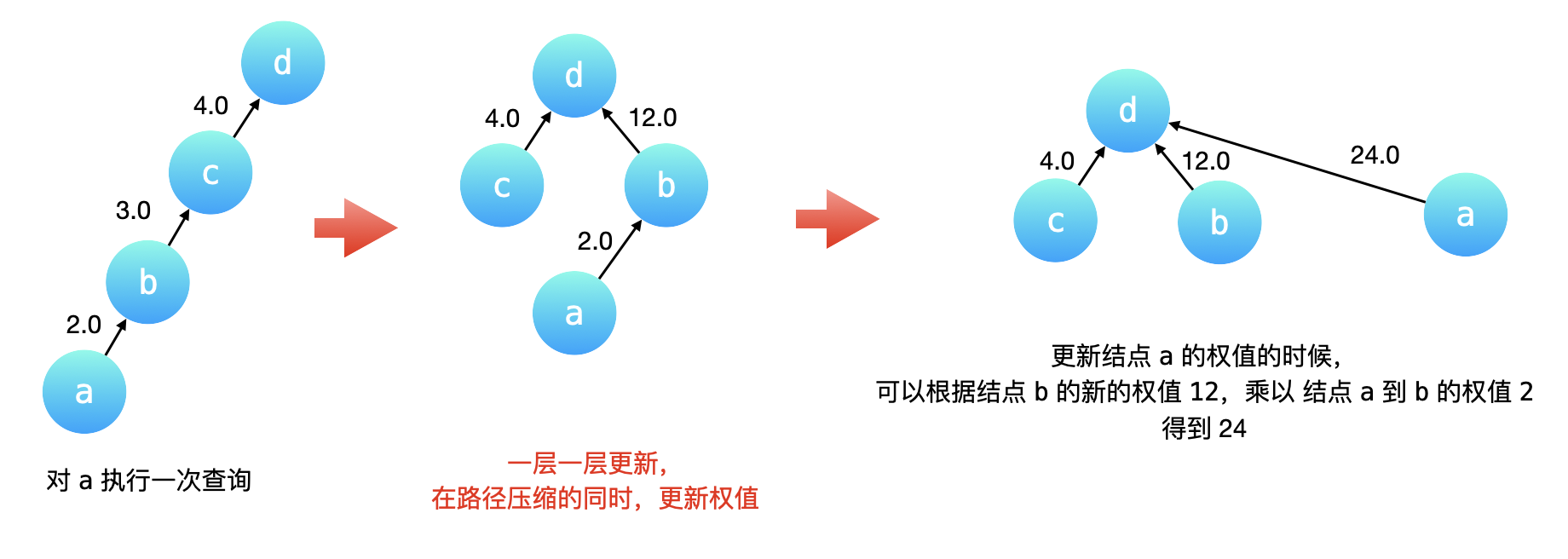
-
如何在「合并」操作中维护权值的变化。
-
合并」操作基于这样一个 很重要的前提:我们将要合并的两棵树的高度最多为 2,换句话说两棵树都必需是「路径压缩」以后的效果,两棵树的叶子结点到根结点最多只需要经过一条有向边。
-
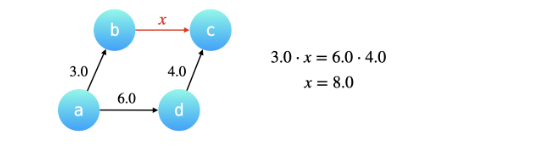
-