Stack/Queue/Heap Exercise 2

1249. Minimum Remove to Make Valid Parentheses

难度中等178

Given a string s of '(' , ')' and lowercase English characters.

Your task is to remove the minimum number of parentheses ( '(' or ')', in any positions ) so that the resulting parentheses string is valid and return any valid string.

Formally, a parentheses string is valid if and only if:

It is the empty string, contains only lowercase characters, or
It can be written as AB (A concatenated with B), where A and B are valid strings, or
It can be written as (A), where A is a valid string.

Example 1:

Input: s = "lee(t(c)o)de)"
Output: "lee(t(c)o)de"
Explanation: "lee(t(co)de)" , "lee(t(c)ode)" would also be accepted.

Example 2:

Input: s = "a)b(c)d"
Output: "ab(c)d"

Example 3:

Input: s = "))(("
Output: ""
Explanation: An empty string is also valid.

Constraints:

1 <= s.length <= 105
s[i] is either'(' , ')', or lowercase English letter.

通过次数31,175

提交次数53,266

思路：

当且仅当 满足以下条件时，字符串中的括号是平衡的：
1. 字符串中有相同数量的 "(" 和 ")"。
例如，"L(ee)(t(()co)d)e" 是一个平衡的字符串。下图展示该字符串的余量变化情况。
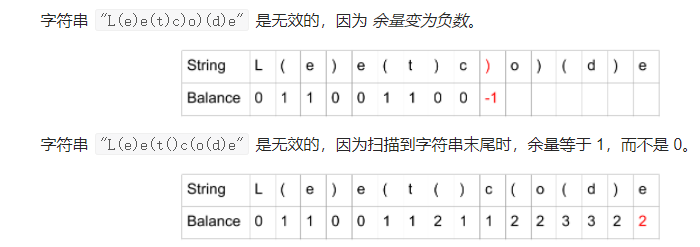
如果最终结果大于0或者中间途中就出现小于0，都是有问题的
该问题要求删除最少括号，使得字符串有效。如何实现该目标？
使用栈，每次遇到 “(“，都将它的索引压入栈中。每次遇到 “)”，都从栈中移除一个索引，用该 “)” 与栈顶的 “(“ 匹配。栈的深度等于余量。需要执行以下操作：
- 如果在栈为空时遇到 “)”，则删除该 “)”，防止余量为负。
- 如果扫描到字符串结尾有 “(“，则删除它，防止余量不为 0
一开始放入1，然后遇到3，就pop
4和5满足栈为空但是是 “)”，必须删除
尽管可以在 O(n)的时间内完成删除操作，但是必须小心，因为一些意外情况会导致 O(n^2），因为一些 O(n)的操作有时也会被误认为是 O(1）。如果在面试中出现这些错误非常不好。
在字符串的任意一个位置添加、删除或更改一个字符的操作都是 O(n)O(n) 的，因为 String 是不可变的。每次修改整个字符串都会重建。

从 list，vector，array 的非最后一个位置添加或删除元素也是 O(n)O(n) 的，因为在其他索引操作需要创建新的空间或者填充空间。

检查一个元素是否在 list 中，常使用线性查找，即使二分查找也要 O(\log n)O(logn) 的复杂度，这并不是理想的效率。
一种安全策略是遍历字符串，然后将要保留的字符插入到 list（Python）。遍历完所有字符后，只需要一步 O(n) 的操作将其转换为字符串。
检查某个元素是否在集合中需要 O(1)
"".join(...) 的复杂度都是 O(n)

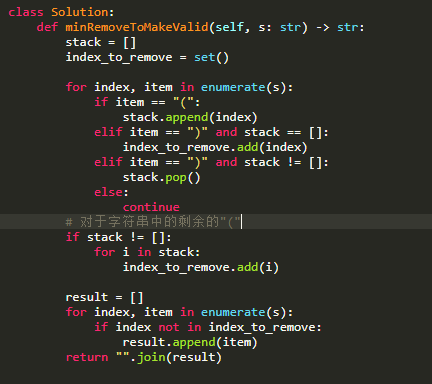
代码：

716. Max Stack

难度简单101

Design a max stack data structure that supports the stack operations and supports finding the stack’s maximum element.

Implement the MaxStack class:

MaxStack() Initializes the stack object.
void push(int x) Pushes element x onto the stack.
int pop() Removes the element on top of the stack and returns it.
int top() Gets the element on the top of the stack without removing it.
int peekMax() Retrieves the maximum element in the stack without removing it.
int popMax() Retrieves the maximum element in the stack and removes it. If there is more than one maximum element, only remove the top-most one.

Example 1:

Input
["MaxStack", "push", "push", "push", "top", "popMax", "top", "peekMax", "pop", "top"]
[[], [5], [1], [5], [], [], [], [], [], []]
Output
[null, null, null, null, 5, 5, 1, 5, 1, 5]

Explanation
MaxStack stk = new MaxStack();
stk.push(5);   // [5] the top of the stack and the maximum number is 5.
stk.push(1);   // [5, 1] the top of the stack is 1, but the maximum is 5.
stk.push(5);   // [5, 1, 5] the top of the stack is 5, which is also the maximum, because it is the top most one.
stk.top();     // return 5, [5, 1, 5] the stack did not change.
stk.popMax();  // return 5, [5, 1] the stack is changed now, and the top is different from the max.
stk.top();     // return 1, [5, 1] the stack did not change.
stk.peekMax(); // return 5, [5, 1] the stack did not change.
stk.pop();     // return 1, [5] the top of the stack and the max element is now 5.
stk.top();     // return 5, [5] the stack did not change.

Constraints:

-107 <= x <= 107
At most 104 calls will be made to push, pop, top, peekMax, and popMax.
There will be at least one element in the stack when pop, top, peekMax, or popMax is called.

Follow up: Could you come up with a solution that supports O(1) for each top call and O(logn) for each other call?

思路：

对于pyhton要做到上述的事情是有一定困难的
一个普通的栈可以支持前三种操作 push(x)，pop() 和 top()，所以我们需要考虑的仅为后两种操作 peekMax() 和 popMax()。

代码：

155. Min Stack

难度简单1280

Design a stack that supports push, pop, top, and retrieving the minimum element in constant time.

Implement the MinStack class:

MinStack() initializes the stack object.
void push(int val) pushes the element val onto the stack.
void pop() removes the element on the top of the stack.
int top() gets the top element of the stack.
int getMin() retrieves the minimum element in the stack.

Example 1:

Input
["MinStack","push","push","push","getMin","pop","top","getMin"]
[[],[-2],[0],[-3],[],[],[],[]]

Output
[null,null,null,null,-3,null,0,-2]

Explanation
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); // return -3
minStack.pop();
minStack.top();    // return 0
minStack.getMin(); // return -2

Constraints:

-231 <= val <= 231 - 1
Methods pop, top and getMin operations will always be called on non-empty stacks.
At most 3 * 104 calls will be made to push, pop, top, and getMin.

时间复杂度为O(1), 空间复杂度为O(N)

224. 基本计算器

难度困难750收藏分享切换为英文接收动态反馈

给你一个字符串表达式 s ，请你实现一个基本计算器来计算并返回它的值。

注意:不允许使用任何将字符串作为数学表达式计算的内置函数，比如 eval() 。

示例 1：

输入：s = "1 + 1"
输出：2

示例 2：

输入：s = " 2-1 + 2 "
输出：3

示例 3：

输入：s = "(1+(4+5+2)-3)+(6+8)"
输出：23

提示：

1 <= s.length <= 3 * 105
s 由数字、'+'、'-'、'('、')'、和 ' ' 组成
s 表示一个有效的表达式
’+’ 不能用作一元运算(例如， “+1” 和 "+(2 + 3)" 无效)
’-‘ 可以用作一元运算(即 “-1” 和 "-(2 + 3)" 是有效的)
输入中不存在两个连续的操作符
每个数字和运行的计算将适合于一个有符号的 32位整数

思路：

好像处理括号匹配的问题常常会用到栈或者队列，感觉有点类似波兰表达式那道题，之后再看看
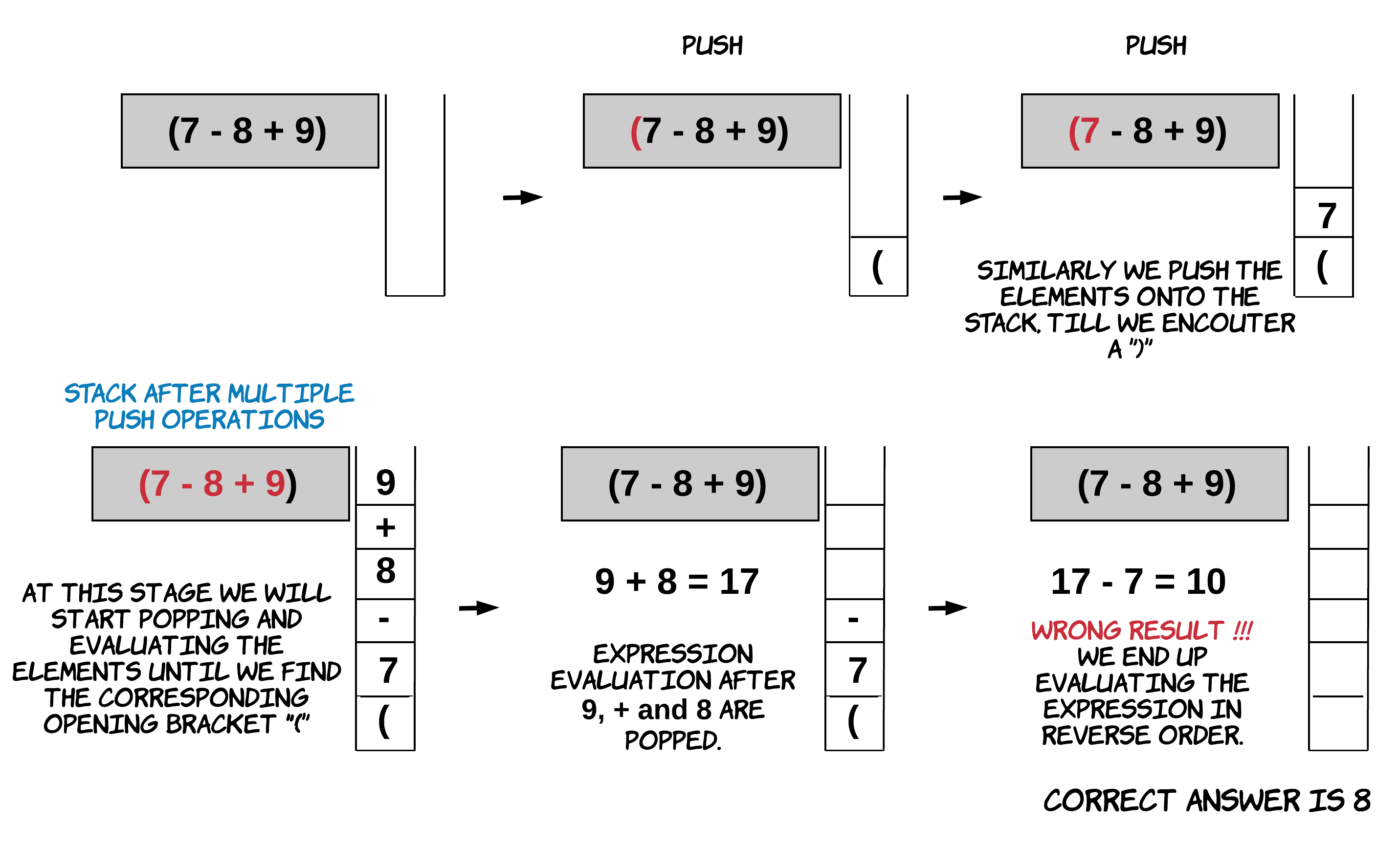
如果我们只是单纯把他插入stack再pop会有问题
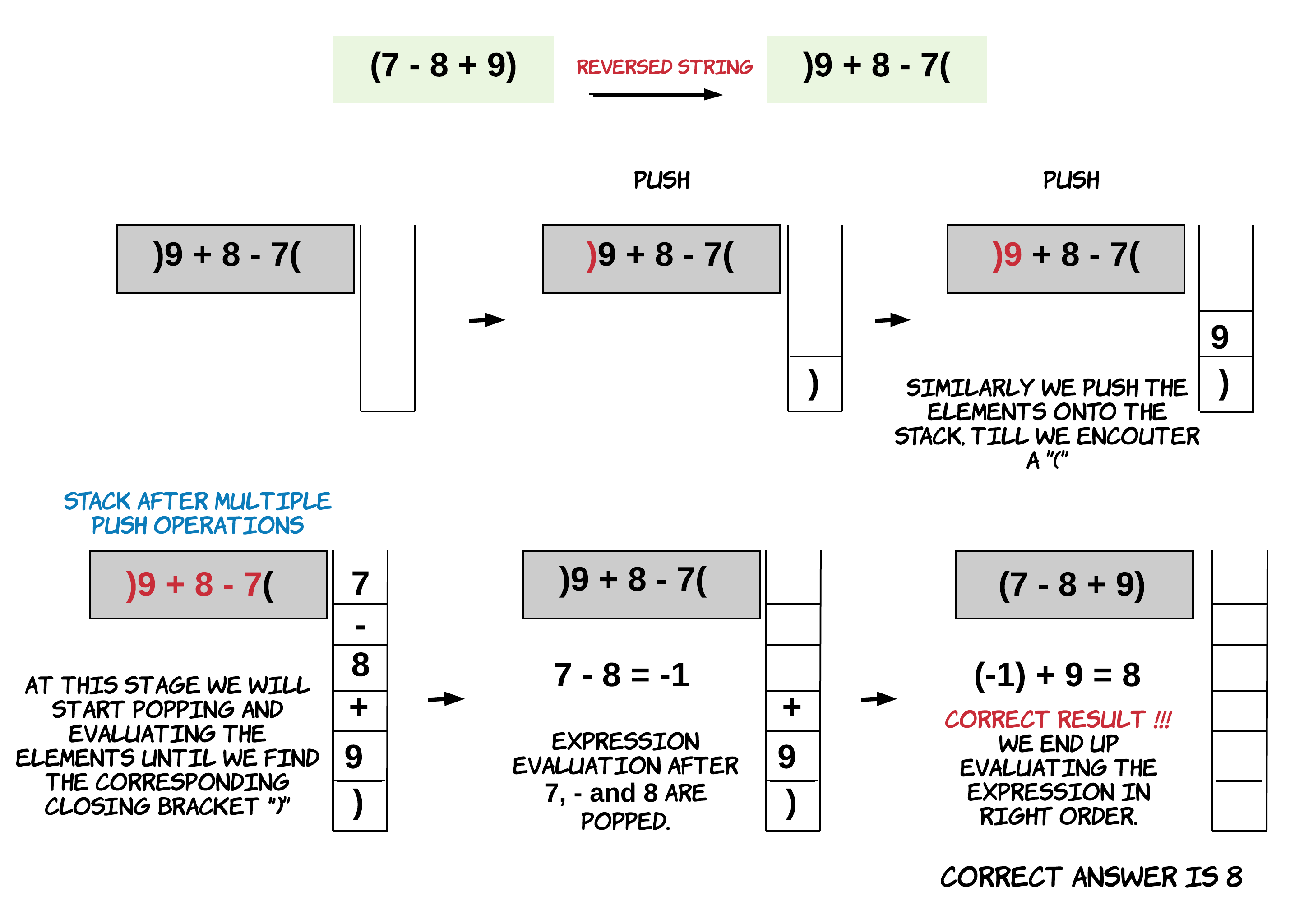
我们应该先取反，再把它push到stack：
Algorithm
- When we encounter an opening parenthesis (, this means an expression just ended.（因为刚刚反转了） Recall we have reversed the expression. So an opening bracket would signify the end of the an expression. This calls for evaluation of the expression by popping operands and operators off the stack till we pop corresponding closing parenthesis. The final result of the expression is pushed back onto the stack.
上面这么做是由于“-”的处理，但是我们可以把“-”和数字绑在一起，用加号连接
例如，对于字符串1+2+(3-(4+5))：
Algorithm
1. Iterate the expression string one character at a time. Since we are reading the expression character by character, we need to be careful when we are reading digits and non-digits.
2. The operands could be formed by multiple characters. A string “123” would mean a numeric 123, which could be formed as: 123 » 120 + 3 » 100 + 20 + 3. Thus, if the character read is a digit we need to form the operand by multiplying 10 to the previously formed continuing operand and adding the digit to it.
3. Whenever we encounter an operator such as + or - we first evaluate the expression to the left and then save this sign for the next evaluation.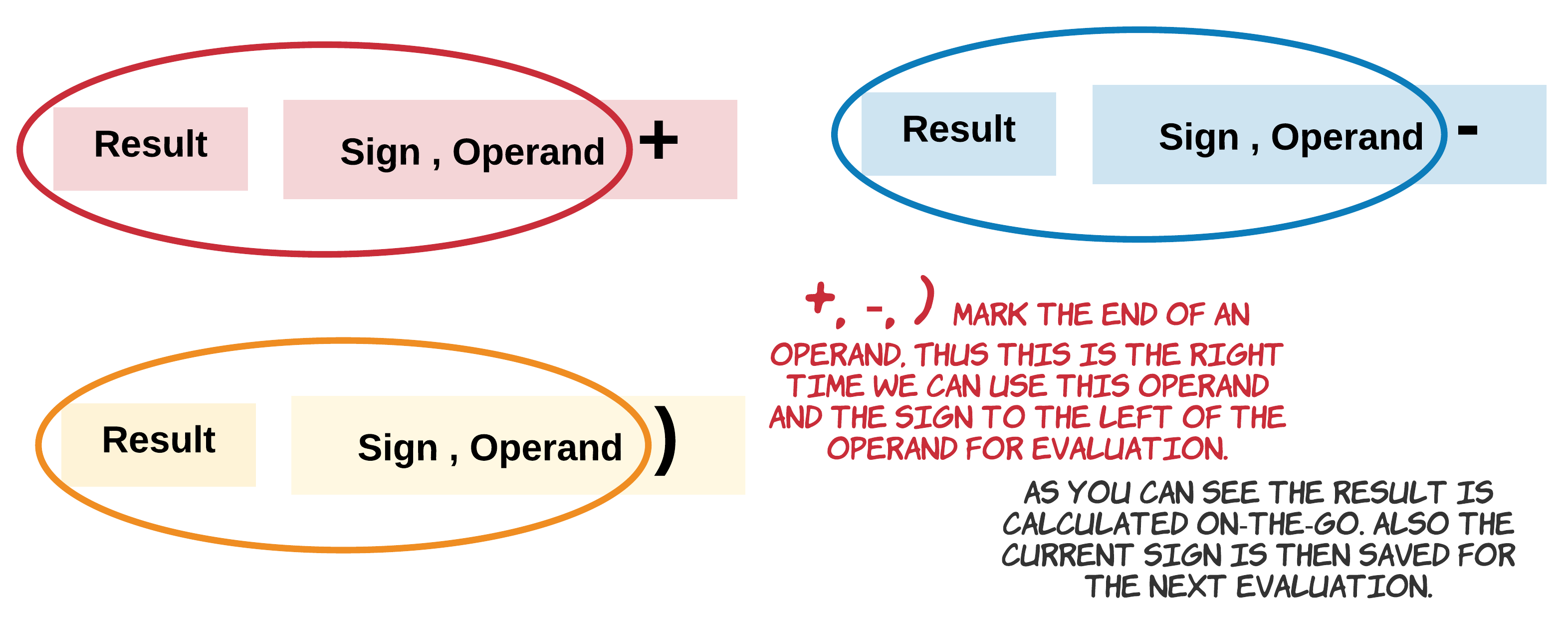
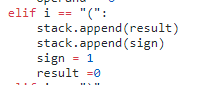
4. If the character is an opening parenthesis (, we just push the result calculated so far and the sign on to the stack (the sign and the magnitude) and start a fresh as if we are calculating a new expression.
5. If the character is a closing parenthesis ), we first calculate the expression to the left. The result from this would be the result of the expression within the set of parenthesis that just concluded. This result is then multiplied with the sign, if there is any on top of the stack. Remember we saved the sign on top of the stack when we had encountered an open parenthesis? This sign is associated with the parenthesis that started then, thus when the expression ends or concludes, we pop the sign and multiply it with result of the expression. It is then just added to the next element on top of the stack.
  - 如果字符是闭合括号），则首先计算左侧的表达式。从此的结果将是刚刚结束的括号内表达式的结果。然后，如果堆栈顶部有任何符号，则此结果将乘以标志。还记得当我们遇到开放括号时，我们将标志保存在堆栈顶部吗？该符号与当时开始的括号相关联，因此，当表达式结束或结论时，我们会弹出符号并乘以表达式的结果。然后仅将其添加到堆栈顶部的下一个元素中。
  - 注意 ( 时，会把 ( 前面的sign和result放进去
对于这个例子，在运行第一个右括号前，stack的样子：
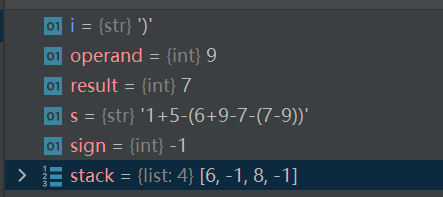
- 可以看到第一个左括号前是负号，所以是6，-1；第二个左括号前是负号，所以是8，-1，然后现在的sign还是存着9前面的负号，当前的result是负号前的7，operand是9
执行完第一个右括号：
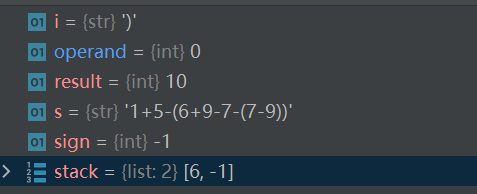
- 先是算出来里面的是-2：result += sign * operand
- 再是pop出来8和-1
- 对于-1是乘法，对于8是加法，所以现在result是10
- 后面也一样，我们可以看到result就够了，operand就是0
- 但是为什么result后面还要加一段呢？
- 因为可能会有1+5这种情况，result只会存一个1，5存在operand里面，这就是安全没有调用stack的情况，就是没有处理括号的情况
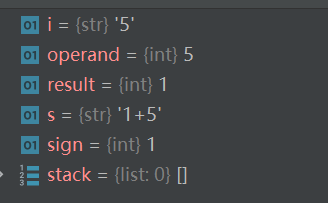
- 所以需要+sign*operand

代码：

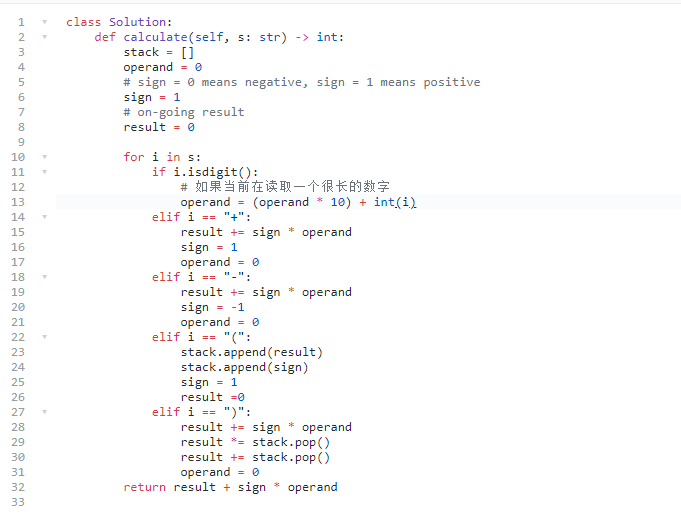
227. 基本计算器 II

难度中等553收藏分享切换为英文接收动态反馈

给你一个字符串表达式 s ，请你实现一个基本计算器来计算并返回它的值。

整数除法仅保留整数部分。

你可以假设给定的表达式总是有效的。所有中间结果将在 [-231, 231 - 1] 的范围内。

注意：不允许使用任何将字符串作为数学表达式计算的内置函数，比如 eval() 。

示例 1：

输入：s = "3+2*2"
输出：7

示例 2：

输入：s = " 3/2 "
输出：1

示例 3：

输入：s = " 3+5 / 2 "
输出：5

提示：

1 <= s.length <= 3 * 105
s 由整数和算符 ('+', '-', '*', '/') 组成，中间由一些空格隔开
s 表示一个 有效表达式
表达式中的所有整数都是非负整数，且在范围 [0, 231 - 1] 内
题目数据保证答案是一个 32-bit 整数

思路：

Meta好像一直对这道题情有独钟
这道题不用进行括号判断
由于乘除优先于加减计算，因此不妨考虑先进行所有乘除运算，并将这些乘除运算后的整数值放回原表达式的相应位置，则随后整个表达式的值，就等于一系列整数加减后的值。
基于此，我们可以用一个栈，保存这些（进行乘除运算后的）整数的值。对于加减号后的数字，将其直接压入栈中；对于乘除号后的数字，可以直接与栈顶元素计算，并替换栈顶元素为计算后的结果。
一开始想和上一题一样直接用i，不用index，但是最后一位还有问题

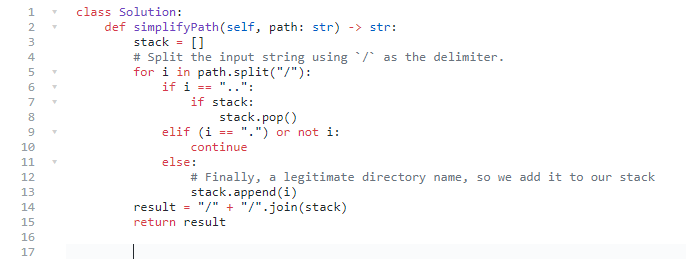
71. 简化路径

难度中等475收藏分享切换为英文接收动态反馈

给你一个字符串 path ，表示指向某一文件或目录的 Unix 风格 绝对路径 （以 '/' 开头），请你将其转化为更加简洁的规范路径。

在 Unix 风格的文件系统中，一个点（.）表示当前目录本身；此外，两个点（..）表示将目录切换到上一级（指向父目录）；两者都可以是复杂相对路径的组成部分。任意多个连续的斜杠（即，'//'）都被视为单个斜杠 '/' 。对于此问题，任何其他格式的点（例如，'...'）均被视为文件/目录名称。

请注意，返回的 规范路径 必须遵循下述格式：

始终以斜杠 '/' 开头。
两个目录名之间必须只有一个斜杠 '/' 。
最后一个目录名（如果存在）不能以 '/' 结尾。
此外，路径仅包含从根目录到目标文件或目录的路径上的目录（即，不含 '.' 或 '..'）。

返回简化后得到的 规范路径 。

示例 1：

输入：path = "/home/"
输出："/home"
解释：注意，最后一个目录名后面没有斜杠。 

示例 2：

输入：path = "/../"
输出："/"
解释：从根目录向上一级是不可行的，因为根目录是你可以到达的最高级。

示例 3：

输入：path = "/home//foo/"
输出："/home/foo"
解释：在规范路径中，多个连续斜杠需要用一个斜杠替换。

示例 4：

输入：path = "/a/./b/../../c/"
输出："/c"

提示：

1 <= path.length <= 3000
path 由英文字母，数字，'.'，'/' 或 '_' 组成。
path 是一个有效的 Unix 风格绝对路径。

思路：

使用stack，在python中是列表
注意 /a/b/c/..是/a/b
Algorithm
1. Initialize a stack, S that we will be using for our implementation.
2. Split the input string using / as the delimiter.
  - This step is really important because no matter what, the given input is a valid path and we simply have to shorten it. So, that means that whatever we have between two / characters is either a directory name or a special character and we have to process them accordingly.
3. Once we are done splitting the input path, we will process one component at a time.
4. If the current component is a . or an empty string, we will do nothing and simply continue.
  - Well if you think about it, the split string array for the string /a//b would be [a,,b]. yes, that’s an empty string in between a and b. Again, from the perspective of the overall path, it doesn’t mean anything.
5. If we encounter a double-dot .., we have to do some processing. This simply means go one level up in the current directory path. So, we will pop an entry from our stack if it’s not empty.
6. Finally, if the component we are processing right now is not one of the special characters, then we will simply add it to our stack because it’s a legitimate directory name.
7. Once we are done processing all the components, we simply have to connect all the directory names in our stack together using / as the delimiter and we will have our shortest path that leads us to the same directory as the one provided as an input.

代码：

Stack/Queue/Heap Exercise 2