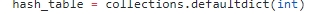Hash Table Exercise 2
1570. Dot Product of Two Sparse Vectors
难度中等20
Given two sparse vectors, compute their dot product.
Implement class SparseVector:
SparseVector(nums)Initializes the object with the vectornumsdotProduct(vec)Compute the dot product between the instance of SparseVector andvec
A sparse vector is a vector that has mostly zero values, you should store the sparse vector efficiently and compute the dot product between two SparseVector.
Follow up: What if only one of the vectors is sparse?
Example 1:
Input: nums1 = [1,0,0,2,3], nums2 = [0,3,0,4,0]
Output: 8
Explanation: v1 = SparseVector(nums1) , v2 = SparseVector(nums2)
v1.dotProduct(v2) = 1*0 + 0*3 + 0*0 + 2*4 + 3*0 = 8
Example 2:
Input: nums1 = [0,1,0,0,0], nums2 = [0,0,0,0,2]
Output: 0
Explanation: v1 = SparseVector(nums1) , v2 = SparseVector(nums2)
v1.dotProduct(v2) = 0*0 + 1*0 + 0*0 + 0*0 + 0*2 = 0
Example 3:
Input: nums1 = [0,1,0,0,2,0,0], nums2 = [1,0,0,0,3,0,4]
Output: 6
Constraints:
n == nums1.length == nums2.length1 <= n <= 10^50 <= nums1[i], nums2[i] <= 100
思路:
- 如果是不考虑稀疏情况,只需要单纯的遍历求和

- 对于稀疏情况,需要记录不为0的部分
- 注意使用.items()来获取值
- 注意是list1.dotProduct(list2),说明self给list1,list2用,dotProduct给list2用
代码:
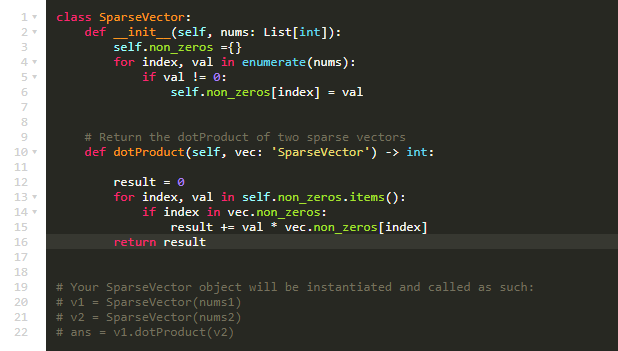
- Time complexity: O(n) for creating the Hash Map; O(L) for calculating the dot product.
- Space complexity: O(L) for creating the Hash Map, as we only store elements that are non-zero. O(1) for calculating the dot product.
1010. Pairs of Songs With Total Durations Divisible by 60
难度中等178
You are given a list of songs where the ith song has a duration of time[i] seconds.
Return the number of pairs of songs for which their total duration in seconds is divisible by 60. Formally, we want the number of indices i, j such that i < j with (time[i] + time[j]) % 60 == 0.
Example 1:
Input: time = [30,20,150,100,40]
Output: 3
Explanation: Three pairs have a total duration divisible by 60:
(time[0] = 30, time[2] = 150): total duration 180
(time[1] = 20, time[3] = 100): total duration 120
(time[1] = 20, time[4] = 40): total duration 60
Example 2:
Input: time = [60,60,60]
Output: 3
Explanation: All three pairs have a total duration of 120, which is divisible by 60.
Constraints:
1 <= time.length <= 6 * 1041 <= time[i] <= 500
思路:
- 最显然的方法是brute force,两层for循环
- 时间复杂度是O(N*2), 空间复杂度是O(1)
- 一开始在想双指针,但显然不是
- 事实上是hash table和一些数学想法,主要是求模的思想
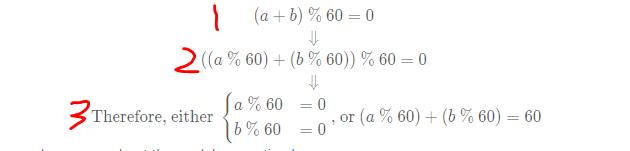
- 如果a和b的和与60求模是0;那么a和b单独和60求模的和在和60求模也是0
- 一个关键点是hash table不是存每个time,而是time%60后的结果
- 分离a和b都是可以mod 60是为了排除hash table[0] and hash table[60]的冲突
- 因为else使用的是互补的逻辑,用60来减i%60

- 使用defaultdict()而不是一般的dict()来保证初始就是0。注意要写入类型是int才会是0
- 第十三行,每次结束要加一,别忘了!面试要注意细节
代码:

- 时间复杂度O(N), 空间复杂度O(1)