Binary Tree Exercise 3

2096. Step-By-Step Directions From a Binary Tree Node to Another

难度中等34

You are given the root of a binary tree with n nodes. Each node is uniquely assigned a value from 1 to n. You are also given an integer startValue representing the value of the start node s, and a different integer destValue representing the value of the destination node t.

Find the shortest path starting from node s and ending at node t. Generate step-by-step directions of such path as a string consisting of only the uppercase letters 'L', 'R', and 'U'. Each letter indicates a specific direction:

'L' means to go from a node to its left child node.
'R' means to go from a node to its right child node.
'U' means to go from a node to its parent node.

Return the step-by-step directions of the shortest path from node s to node t.

Example 1:

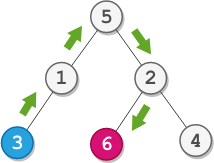
Input: root = [5,1,2,3,null,6,4], startValue = 3, destValue = 6
Output: "UURL"
Explanation: The shortest path is: 3 → 1 → 5 → 2 → 6.

Example 2:

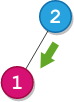
Input: root = [2,1], startValue = 2, destValue = 1
Output: "L"
Explanation: The shortest path is: 2 → 1.

Constraints:

The number of nodes in the tree is n.
2 <= n <= 105
1 <= Node.val <= n
All the values in the tree are unique.
1 <= startValue, destValue <= n
startValue != destValue

1740. 找到二叉树中的距离

难度中等14

给定一棵二叉树的根节点 root 以及两个整数 p 和 q ，返回该二叉树中值为 p 的结点与值为 q 的结点间的距离。

两个结点间的距离就是从一个结点到另一个结点的路径上边的数目。

示例 1：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 0
输出：3
解释：在 5 和 0 之间有 3 条边：5-3-1-0

示例 2：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 7
输出：2
解释：在 5 和 7 之间有 2 条边：5-2-7

示例 3：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 5
输出：0
解释：一个结点与它本身之间的距离为 0

提示：

树中结点个数的范围在 [1, 104].
0 <= Node.val <= 109
树中所有结点的值都是唯一的.
p 和q 是树中结点的值.

938. 二叉搜索树的范围和

难度简单286

给定二叉搜索树的根结点 root，返回值位于范围 [low, high] 之间的所有结点的值的和。

示例 1：

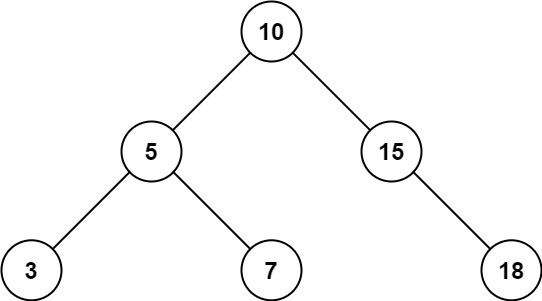
输入：root = [10,5,15,3,7,null,18], low = 7, high = 15
输出：32

示例 2：

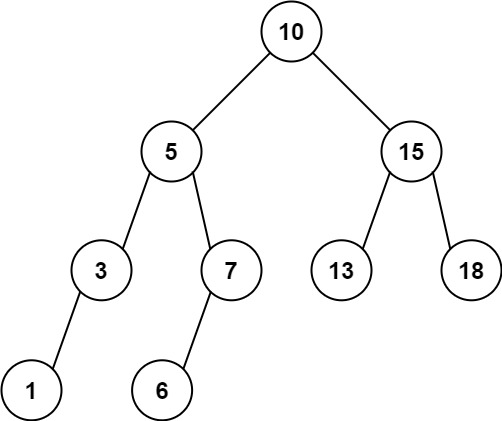
输入：root = [10,5,15,3,7,13,18,1,null,6], low = 6, high = 10
输出：23

提示：

树中节点数目在范围 [1, 2 * 104] 内
1 <= Node.val <= 105
1 <= low <= high <= 105
所有 Node.val 互不相同

987. 二叉树的垂序遍历

难度困难189

给你二叉树的根结点 root ，请你设计算法计算二叉树的 垂序遍历 序列。

对位于 (row, col) 的每个结点而言，其左右子结点分别位于 (row + 1, col - 1) 和 (row + 1, col + 1) 。树的根结点位于 (0, 0) 。

二叉树的 垂序遍历 从最左边的列开始直到最右边的列结束，按列索引每一列上的所有结点，形成一个按出现位置从上到下排序的有序列表。如果同行同列上有多个结点，则按结点的值从小到大进行排序。

返回二叉树的 垂序遍历 序列。

示例 1：

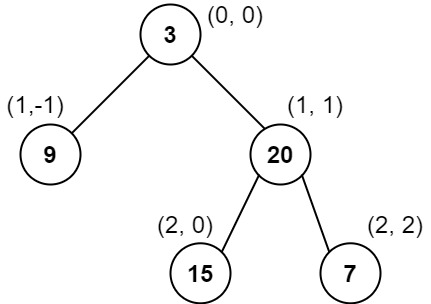
输入：root = [3,9,20,null,null,15,7]
输出：[[9],[3,15],[20],[7]]
解释：
列 -1 ：只有结点 9 在此列中。
列  0 ：只有结点 3 和 15 在此列中，按从上到下顺序。
列  1 ：只有结点 20 在此列中。
列  2 ：只有结点 7 在此列中。

示例 2：

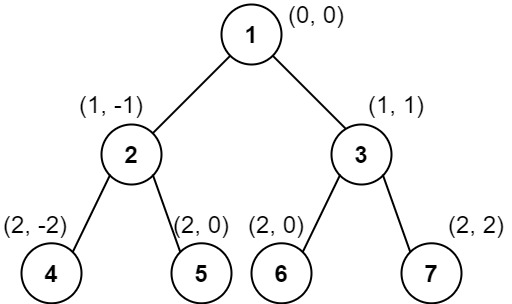
输入：root = [1,2,3,4,5,6,7]
输出：[[4],[2],[1,5,6],[3],[7]]
解释：
列 -2 ：只有结点 4 在此列中。
列 -1 ：只有结点 2 在此列中。
列  0 ：结点 1 、5 和 6 都在此列中。
          1 在上面，所以它出现在前面。
          5 和 6 位置都是 (2, 0) ，所以按值从小到大排序，5 在 6 的前面。
列  1 ：只有结点 3 在此列中。
列  2 ：只有结点 7 在此列中。

示例 3：

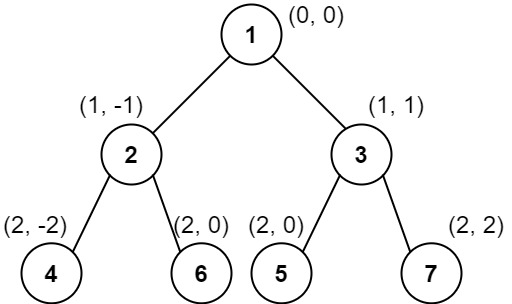
输入：root = [1,2,3,4,6,5,7]
输出：[[4],[2],[1,5,6],[3],[7]]
解释：
这个示例实际上与示例 2 完全相同，只是结点 5 和 6 在树中的位置发生了交换。
因为 5 和 6 的位置仍然相同，所以答案保持不变，仍然按值从小到大排序。

提示：

树中结点数目总数在范围 [1, 1000] 内
0 <= Node.val <= 1000

426. 将二叉搜索树转化为排序的双向链表

难度中等165

将一个 二叉搜索树 就地转化为一个 已排序的双向循环链表 。

对于双向循环列表，你可以将左右孩子指针作为双向循环链表的前驱和后继指针，第一个节点的前驱是最后一个节点，最后一个节点的后继是第一个节点。

特别地，我们希望可以就地完成转换操作。当转化完成以后，树中节点的左指针需要指向前驱，树中节点的右指针需要指向后继。还需要返回链表中最小元素的指针。

示例 1：

输入：root = [4,2,5,1,3] 

输出：[1,2,3,4,5]

解释：下图显示了转化后的二叉搜索树，实线表示后继关系，虚线表示前驱关系。

示例 2：

输入：root = [2,1,3]
输出：[1,2,3]

示例 3：

输入：root = []
输出：[]
解释：输入是空树，所以输出也是空链表。

示例 4：

输入：root = [1]
输出：[1]

提示：

-1000 <= Node.val <= 1000
Node.left.val < Node.val < Node.right.val
Node.val 的所有值都是独一无二的
0 <= Number of Nodes <= 2000

543. Diameter of Binary Tree

难度简单1019

Given the root of a binary tree, return the length of the diameter of the tree.

The diameter of a binary tree is the length of the longest path between any two nodes in a tree. This path may or may not pass through the root.

The length of a path between two nodes is represented by the number of edges between them.

Example 1:

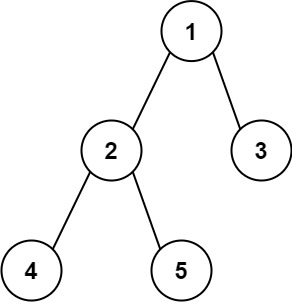
Input: root = [1,2,3,4,5]
Output: 3
Explanation: 3 is the length of the path [4,2,1,3] or [5,2,1,3].

Example 2:

Input: root = [1,2]
Output: 1

Constraints:

The number of nodes in the tree is in the range [1, 104].
-100 <= Node.val <= 100

173. Binary Search Tree Iterator

难度中等591

Implement the BSTIterator class that represents an iterator over the in-order traversal of a binary search tree (BST):

BSTIterator(TreeNode root) Initializes an object of the BSTIterator class. The root of the BST is given as part of the constructor. The pointer should be initialized to a non-existent number smaller than any element in the BST.
boolean hasNext() Returns true if there exists a number in the traversal to the right of the pointer, otherwise returns false.
int next() Moves the pointer to the right, then returns the number at the pointer.

Notice that by initializing the pointer to a non-existent smallest number, the first call to next() will return the smallest element in the BST.

You may assume that next() calls will always be valid. That is, there will be at least a next number in the in-order traversal when next() is called.

Example 1:

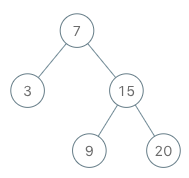
Input
["BSTIterator", "next", "next", "hasNext", "next", "hasNext", "next", "hasNext", "next", "hasNext"]
[[[7, 3, 15, null, null, 9, 20]], [], [], [], [], [], [], [], [], []]
Output
[null, 3, 7, true, 9, true, 15, true, 20, false]

Explanation
BSTIterator bSTIterator = new BSTIterator([7, 3, 15, null, null, 9, 20]);
bSTIterator.next();    // return 3
bSTIterator.next();    // return 7
bSTIterator.hasNext(); // return True
bSTIterator.next();    // return 9
bSTIterator.hasNext(); // return True
bSTIterator.next();    // return 15
bSTIterator.hasNext(); // return True
bSTIterator.next();    // return 20
bSTIterator.hasNext(); // return False

Constraints:

The number of nodes in the tree is in the range [1, 105].
0 <= Node.val <= 106
At most 105 calls will be made to hasNext, and next.

Follow up:

Could you implement next() and hasNext() to run in average O(1) time and use O(h) memory, where h is the height of the tree?

129. Sum Root to Leaf Numbers

难度中等522

You are given the root of a binary tree containing digits from 0 to 9 only.

Each root-to-leaf path in the tree represents a number.

For example, the root-to-leaf path 1 -> 2 -> 3 represents the number 123.

Return the total sum of all root-to-leaf numbers. Test cases are generated so that the answer will fit in a 32-bit integer.

A leaf node is a node with no children.

Example 1:

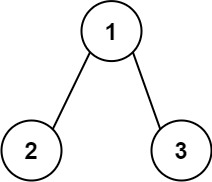
Input: root = [1,2,3]
Output: 25
Explanation:
The root-to-leaf path 1->2 represents the number 12.
The root-to-leaf path 1->3 represents the number 13.
Therefore, sum = 12 + 13 = 25.

Example 2:

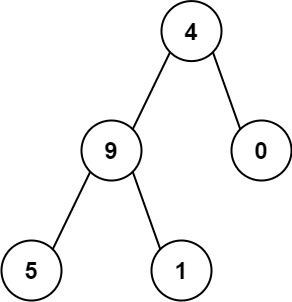
Input: root = [4,9,0,5,1]
Output: 1026
Explanation:
The root-to-leaf path 4->9->5 represents the number 495.
The root-to-leaf path 4->9->1 represents the number 491.
The root-to-leaf path 4->0 represents the number 40.
Therefore, sum = 495 + 491 + 40 = 1026.

Constraints:

The number of nodes in the tree is in the range [1, 1000].
0 <= Node.val <= 9
The depth of the tree will not exceed 10.

270. Closest Binary Search Tree Value

难度简单112

Given the root of a binary search tree and a target value, return the value in the BST that is closest to the target.

Example 1:

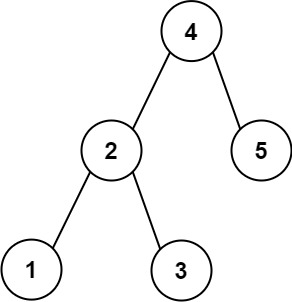
Input: root = [4,2,5,1,3], target = 3.714286
Output: 4

Example 2:

Input: root = [1], target = 4.428571
Output: 1

Constraints:

The number of nodes in the tree is in the range [1, 104].
0 <= Node.val <= 109
-109 <= target <= 109

863. All Nodes Distance K in Binary Tree

难度中等533

Given the root of a binary tree, the value of a target node target, and an integer k, return an array of the values of all nodes that have a distance k from the target node.

You can return the answer in any order.

Example 1:

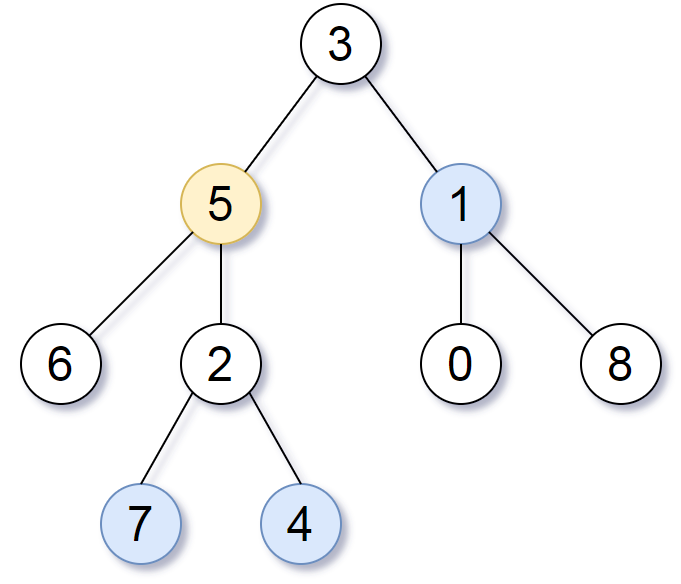
Input: root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, k = 2
Output: [7,4,1]
Explanation: The nodes that are a distance 2 from the target node (with value 5) have values 7, 4, and 1.

Example 2:

Input: root = [1], target = 1, k = 3
Output: []

Constraints:

The number of nodes in the tree is in the range [1, 500].
0 <= Node.val <= 500
All the values Node.val are unique.
target is the value of one of the nodes in the tree.
0 <= k <= 1000

536. Construct Binary Tree from String

难度中等83

You need to construct a binary tree from a string consisting of parenthesis and integers.

The whole input represents a binary tree. It contains an integer followed by zero, one or two pairs of parenthesis. The integer represents the root’s value and a pair of parenthesis contains a child binary tree with the same structure.

You always start to construct the left child node of the parent first if it exists.

Example 1:

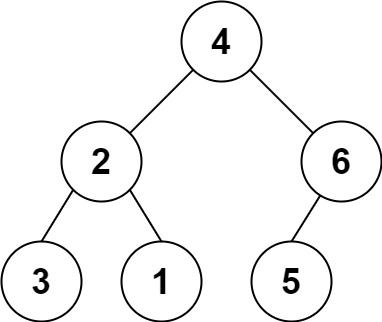
Input: s = "4(2(3)(1))(6(5))"
Output: [4,2,6,3,1,5]

Example 2:

Input: s = "4(2(3)(1))(6(5)(7))"
Output: [4,2,6,3,1,5,7]

Example 3:

Input: s = "-4(2(3)(1))(6(5)(7))"
Output: [-4,2,6,3,1,5,7]

Constraints:

0 <= s.length <= 3 * 104
s consists of digits, '(', ')', and '-' only.

124. Binary Tree Maximum Path Sum

难度困难1566

A path in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence at most once. Note that the path does not need to pass through the root.

The path sum of a path is the sum of the node’s values in the path.

Given the root of a binary tree, return the maximum path sum of any non-empty path.

Example 1:

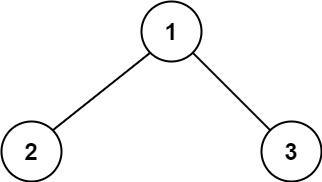
Input: root = [1,2,3]
Output: 6
Explanation: The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.

Example 2:

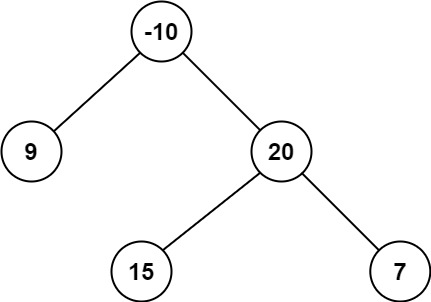
Input: root = [-10,9,20,null,null,15,7]
Output: 42
Explanation: The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.

Constraints:

The number of nodes in the tree is in the range [1, 3 * 104].
-1000 <= Node.val <= 1000

272. Closest Binary Search Tree Value II

难度困难105

Given the root of a binary search tree, a target value, and an integer k, return the k values in the BST that are closest to the target. You may return the answer in any order.

You are guaranteed to have only one unique set of k values in the BST that are closest to the target.

Example 1:

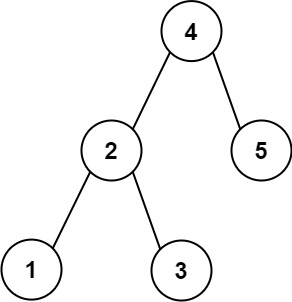
Input: root = [4,2,5,1,3], target = 3.714286, k = 2
Output: [4,3]

Example 2:

Input: root = [1], target = 0.000000, k = 1
Output: [1]

Constraints:

The number of nodes in the tree is n.
1 <= k <= n <= 104.
0 <= Node.val <= 109
-109 <= target <= 109

Follow up: Assume that the BST is balanced. Could you solve it in less than O(n) runtime (where n = total nodes)?

428. Serialize and Deserialize N-ary Tree

难度困难88

Serialization is the process of converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.

Design an algorithm to serialize and deserialize an N-ary tree. An N-ary tree is a rooted tree in which each node has no more than N children. There is no restriction on how your serialization/deserialization algorithm should work. You just need to ensure that an N-ary tree can be serialized to a string and this string can be deserialized to the original tree structure.

For example, you may serialize the following 3-ary tree

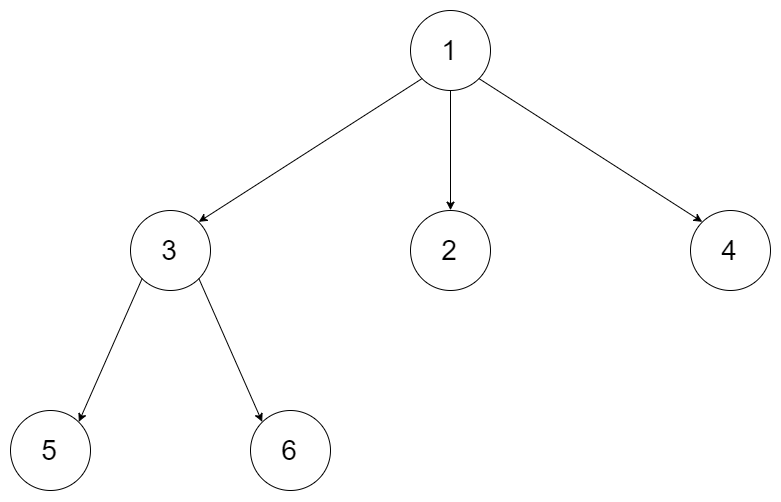
as [1 [3[5 6] 2 4]]. Note that this is just an example, you do not necessarily need to follow this format.

Or you can follow LeetCode’s level order traversal serialization format, where each group of children is separated by the null value.

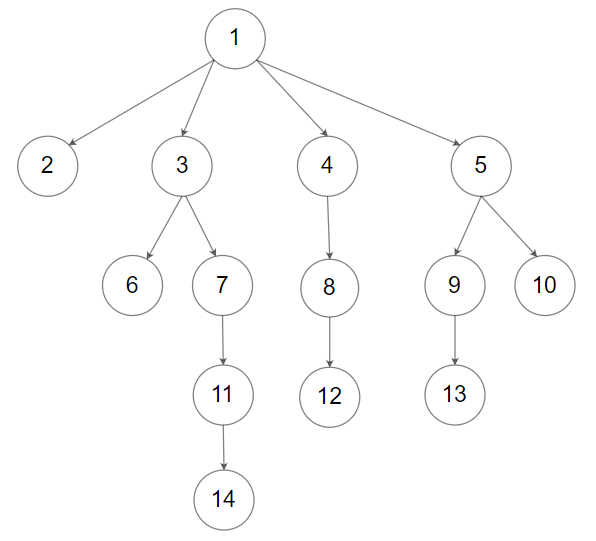
For example, the above tree may be serialized as [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14].

You do not necessarily need to follow the above-suggested formats, there are many more different formats that work so please be creative and come up with different approaches yourself.

Example 1:

Input: root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
Output: [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]

Example 2:

Input: root = [1,null,3,2,4,null,5,6]
Output: [1,null,3,2,4,null,5,6]

Example 3:

Input: root = []
Output: []

Constraints:

The number of nodes in the tree is in the range [0, 104].
0 <= Node.val <= 104
The height of the n-ary tree is less than or equal to 1000
Do not use class member/global/static variables to store states. Your encode and decode algorithms should be stateless.

297. Serialize and Deserialize Binary Tree

难度困难855

Design an algorithm to serialize and deserialize a binary tree. There is no restriction on how your serialization/deserialization algorithm should work. You just need to ensure that a binary tree can be serialized to a string and this string can be deserialized to the original tree structure.

Clarification: The input/output format is the same as how LeetCode serializes a binary tree. You do not necessarily need to follow this format, so please be creative and come up with different approaches yourself.

Example 1:

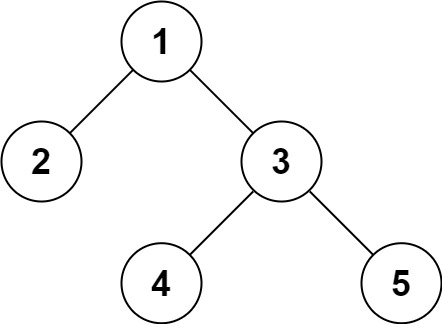
Input: root = [1,2,3,null,null,4,5]
Output: [1,2,3,null,null,4,5]

Example 2:

Input: root = []
Output: []

Constraints:

The number of nodes in the tree is in the range [0, 104].
-1000 <= Node.val <= 1000

366. Find Leaves of Binary Tree

难度中等172

Given the root of a binary tree, collect a tree’s nodes as if you were doing this:

Collect all the leaf nodes.
Remove all the leaf nodes.
Repeat until the tree is empty.

Example 1:

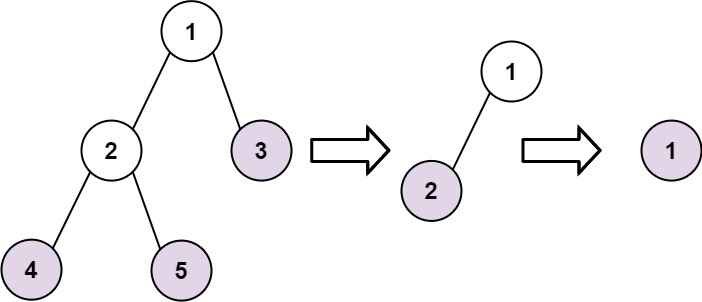
Input: root = [1,2,3,4,5]
Output: [[4,5,3],[2],[1]]
Explanation:
[[3,5,4],[2],[1]] and [[3,4,5],[2],[1]] are also considered correct answers since per each level it does not matter the order on which elements are returned.

Example 2:

Input: root = [1]
Output: [[1]]

Constraints:

The number of nodes in the tree is in the range [1, 100].
-100 <= Node.val <= 100

103. Binary Tree Zigzag Level Order Traversal

难度中等633

Given the root of a binary tree, return the zigzag level order traversal of its nodes’ values. (i.e., from left to right, then right to left for the next level and alternate between).

Example 1:

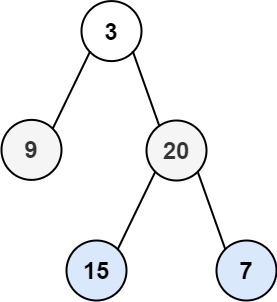
Input: root = [3,9,20,null,null,15,7]
Output: [[3],[20,9],[15,7]]

Example 2:

Input: root = [1]
Output: [[1]]

Example 3:

Input: root = []
Output: []

Constraints:

The number of nodes in the tree is in the range [0, 2000].
-100 <= Node.val <= 100

427. Construct Quad Tree

难度中等156

Given a n * n matrix grid of 0's and 1's only. We want to represent the grid with a Quad-Tree.

Return the root of the Quad-Tree representing the grid.

Notice that you can assign the value of a node to True or False when isLeaf is False, and both are accepted in the answer.

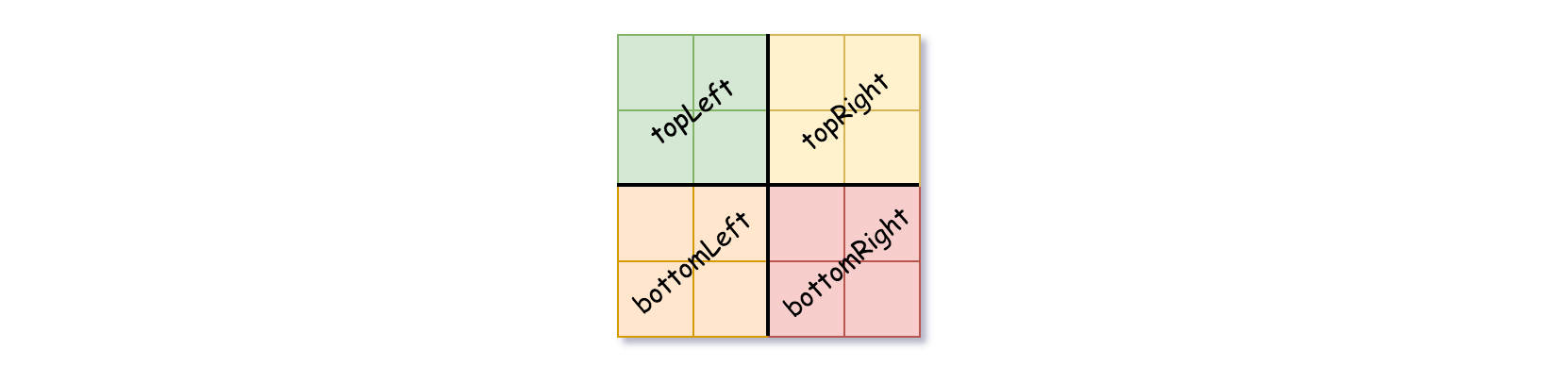
A Quad-Tree is a tree data structure in which each internal node has exactly four children. Besides, each node has two attributes:

val: True if the node represents a grid of 1’s or False if the node represents a grid of 0’s.
isLeaf: True if the node is leaf node on the tree or False if the node has the four children.

class Node {
    public boolean val;
    public boolean isLeaf;
    public Node topLeft;
    public Node topRight;
    public Node bottomLeft;
    public Node bottomRight;
}

We can construct a Quad-Tree from a two-dimensional area using the following steps:

If the current grid has the same value (i.e all 1's or all 0's) set isLeaf True and set val to the value of the grid and set the four children to Null and stop.
If the current grid has different values, set isLeaf to False and set val to any value and divide the current grid into four sub-grids as shown in the photo.
Recurse for each of the children with the proper sub-grid.

If you want to know more about the Quad-Tree, you can refer to the wiki.

Quad-Tree format:

The output represents the serialized format of a Quad-Tree using level order traversal, where null signifies a path terminator where no node exists below.

It is very similar to the serialization of the binary tree. The only difference is that the node is represented as a list [isLeaf, val].

If the value of isLeaf or val is True we represent it as 1 in the list [isLeaf, val] and if the value of isLeaf or val is False we represent it as 0.

Example 1:

Input: grid = [[0,1],[1,0]]
Output: [[0,1],[1,0],[1,1],[1,1],[1,0]]
Explanation: The explanation of this example is shown below:
Notice that 0 represnts False and 1 represents True in the photo representing the Quad-Tree.

Example 2:

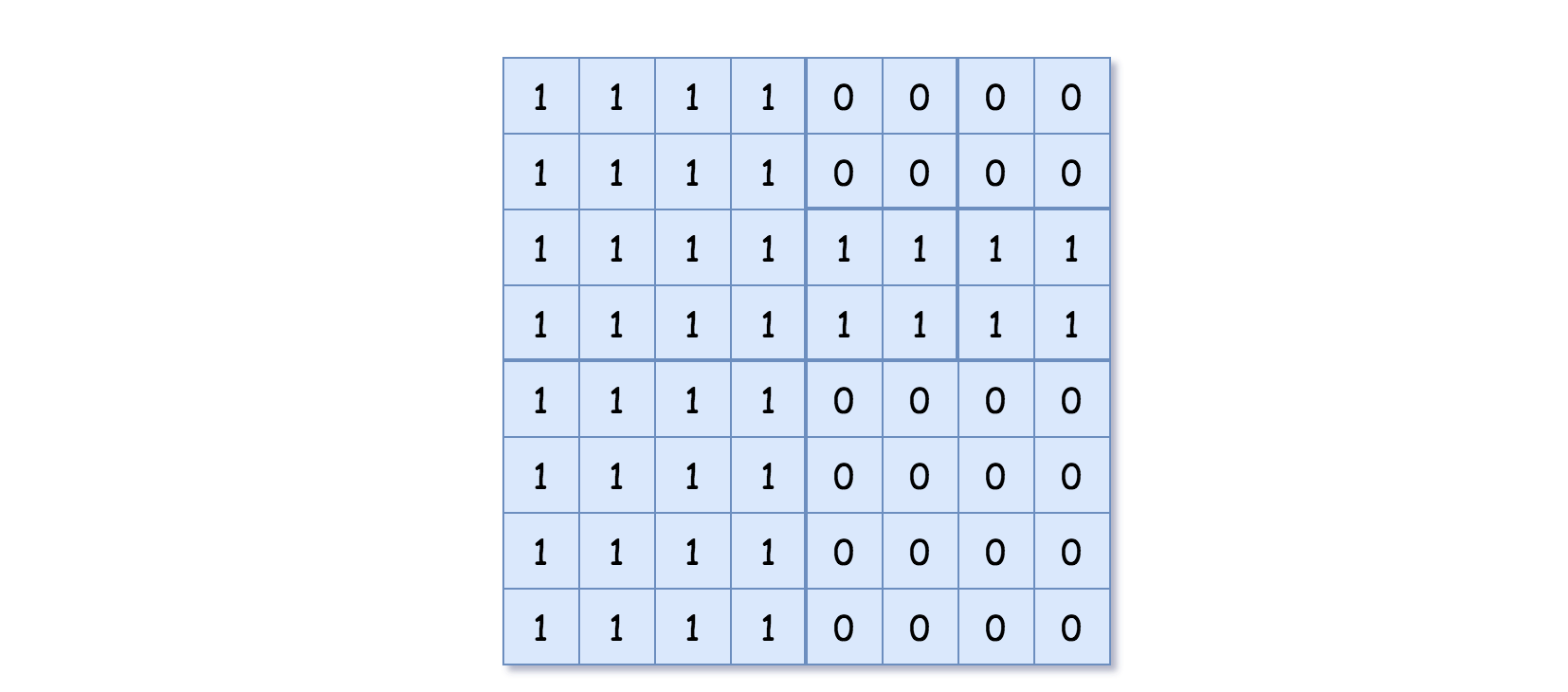
Input: grid = [[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0],[1,1,1,1,1,1,1,1],[1,1,1,1,1,1,1,1],[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0]]
Output: [[0,1],[1,1],[0,1],[1,1],[1,0],null,null,null,null,[1,0],[1,0],[1,1],[1,1]]
Explanation: All values in the grid are not the same. We divide the grid into four sub-grids.
The topLeft, bottomLeft and bottomRight each has the same value.
The topRight have different values so we divide it into 4 sub-grids where each has the same value.
Explanation is shown in the photo below:

Constraints:

n == grid.length == grid[i].length
n == 2x where 0 <= x <= 6

Binary Tree Exercise 3