Binary Tree Exercise 2
1.1 深度优先遍历使用的数据结构(栈):
在深度优先遍历的过程中,需要将 当前遍历到的结点 的相邻结点 暂时保存 起来,以便在回退的时候可以继续访问它们。遍历到的结点的顺序呈现「后进先出」的特点,因此 深度优先遍历可以通过「栈」实现。
在Python中,列表就满足后进先出的要求(append,pop)
对于之前做过的二叉树的前中后序遍历,使用recursion(递归)是很容易想到的,但是使用iteration是比较难的,也是可能会被作为follow up的考点。推荐DFS都使用recursion来实现

主要是掌握前中后序的迭代和递归写法
1.2 广度优先遍历使用的数据结构(队列):
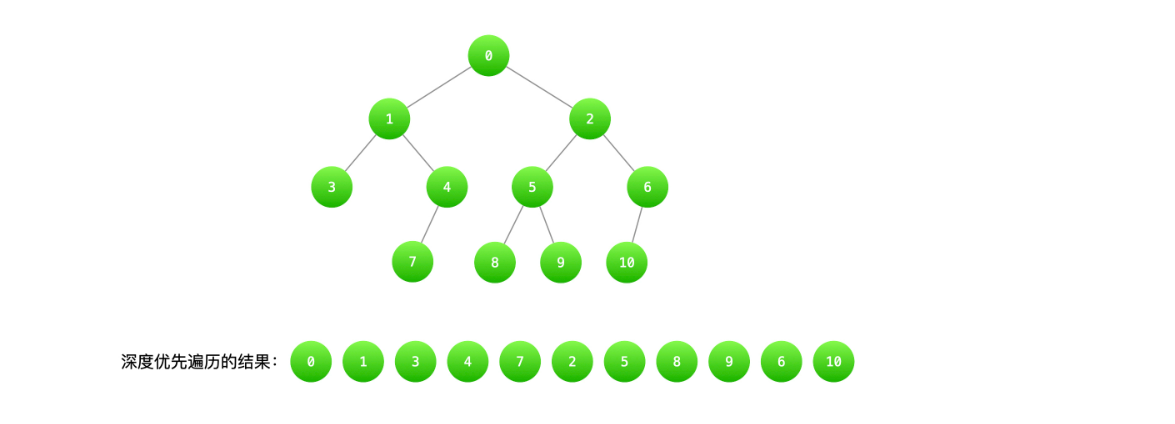
1.3 树的深度优先搜索:
- 「根结点 → 右子树 → 左子树」
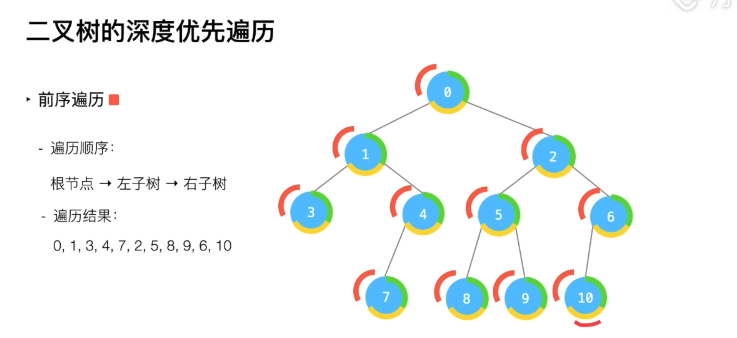
- 前序(preorder)遍历:
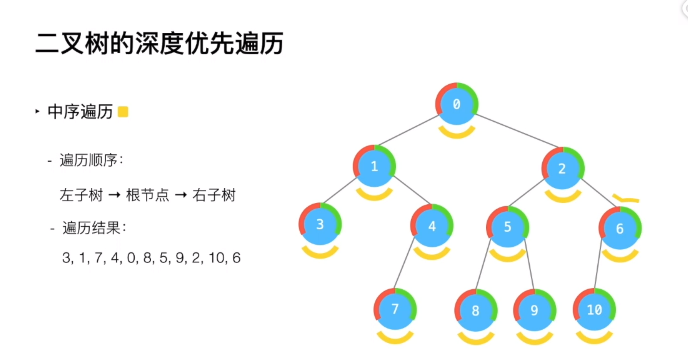
- 中序(Inorder)遍历
- 后序(Posorder)遍历
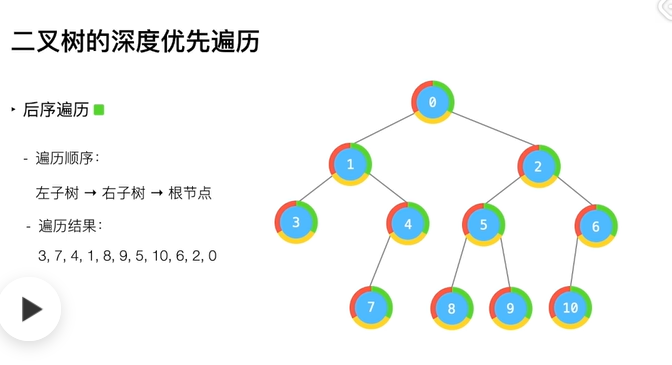
后序遍历最为重要
Preorder Binary Tree (Iteration)
- 前序遍历是中左右;
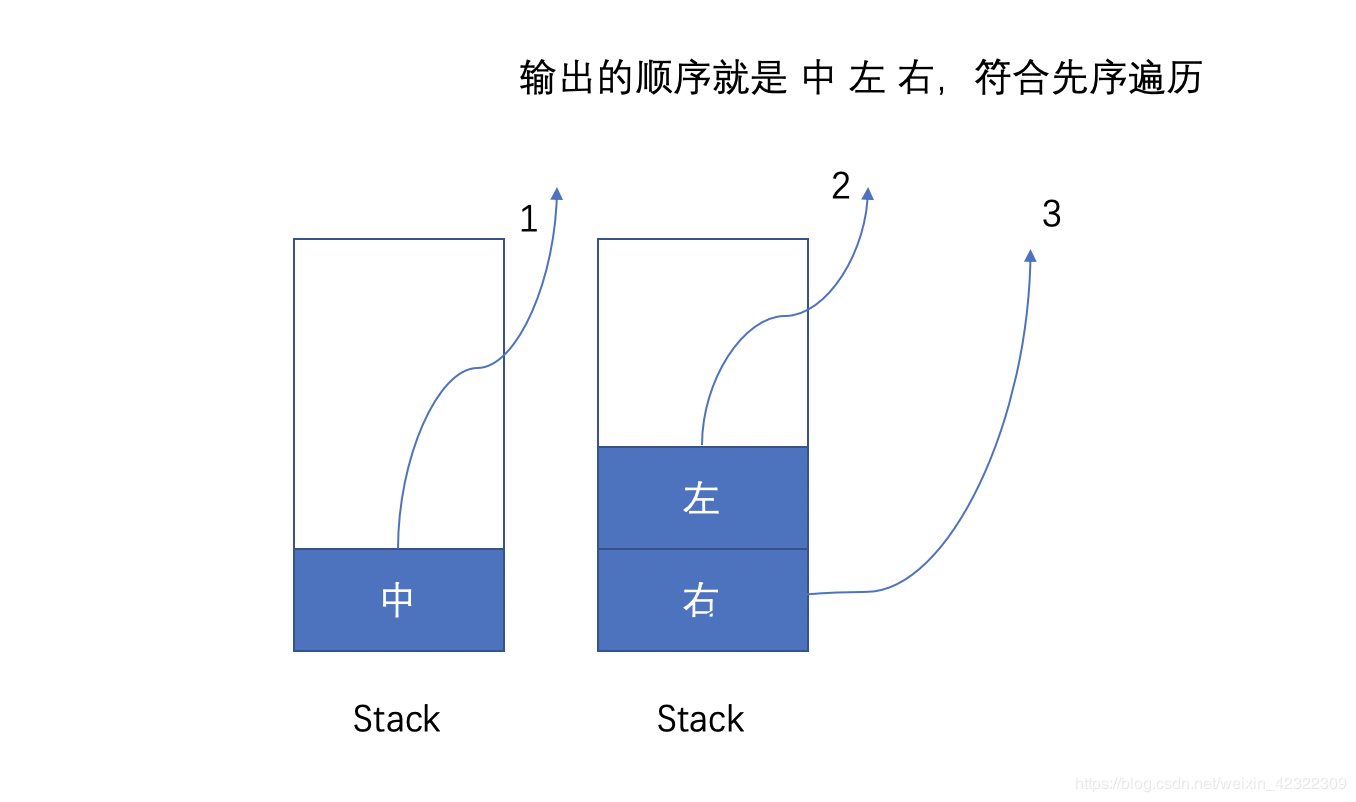
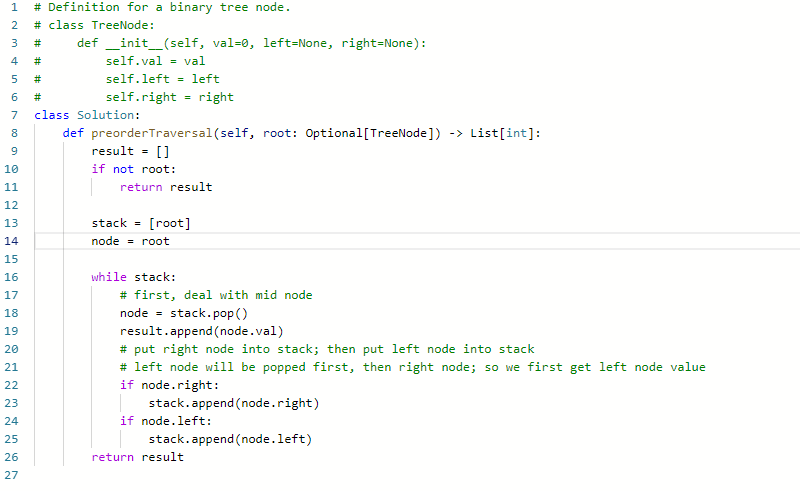
Preorder Binary Tree (Recursion)
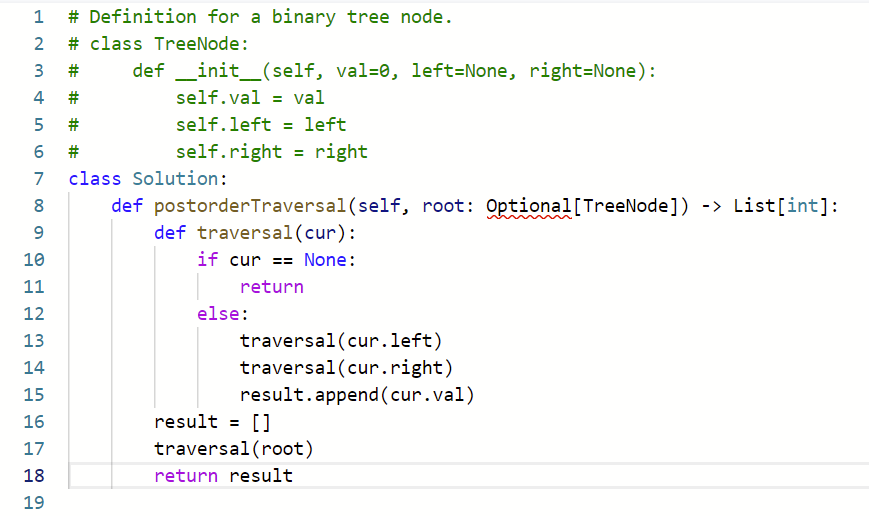
Postorder Binary Tree (Iteration)
- 对于后序遍历的迭代法,就基本改一下前序遍历中的内容即可
- 前序遍历是中左右,后序遍历是左右中
- 那么我们只需要压入左右时和前序换一下,先压入左再压入右
- 最后反转数组
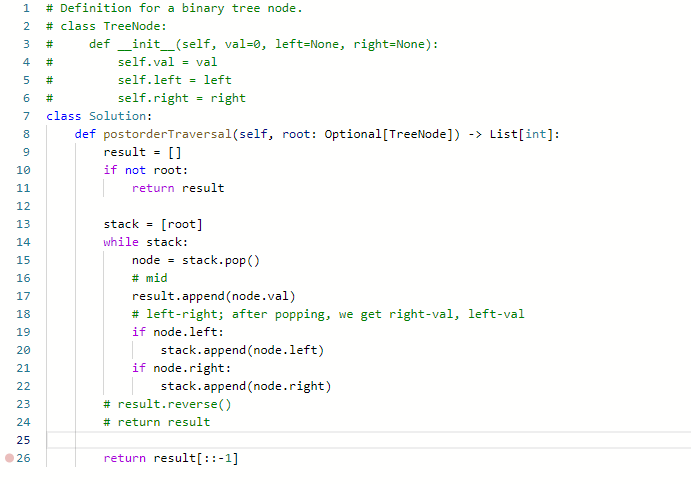
注意不可以return list.reverse()
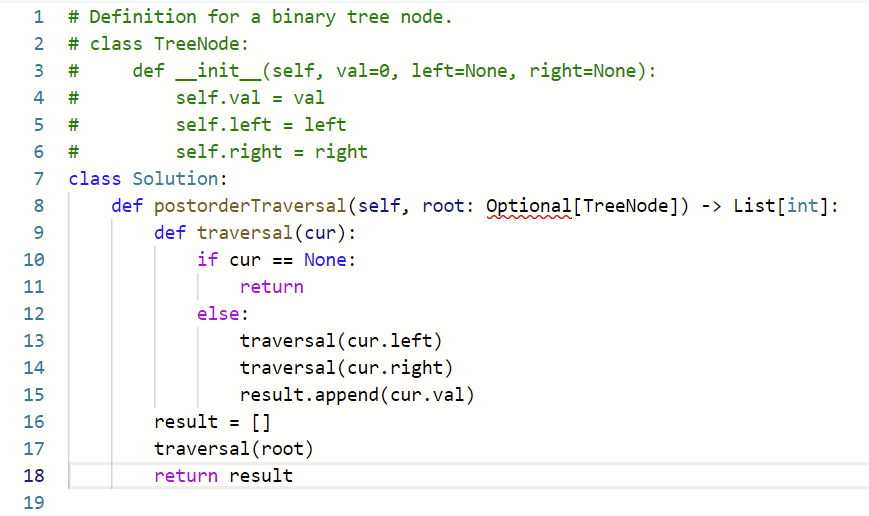
Postorder Binary Tree (Recursion)
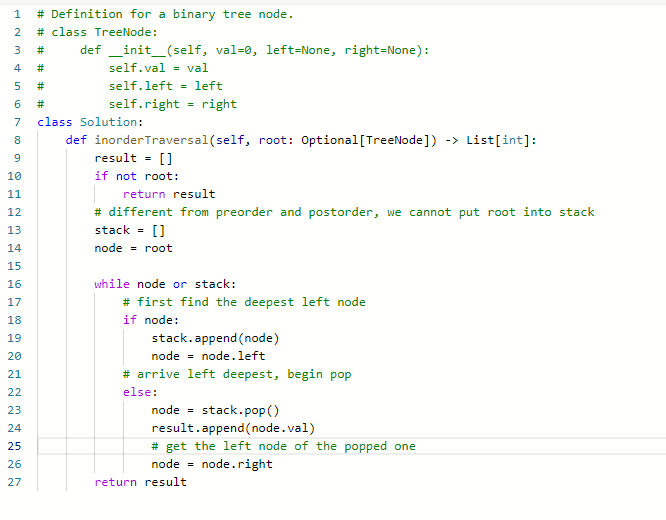
Inorder Binary Tree (Iteration)
- 前序遍历的顺序是中左右, 而对于一个binary tree, 先访问的元素是中间节点,要处理的元素也是中间节点。前序要访问的元素和要处理的元素顺序是一致的,都是中间节点。
- 中序遍历的顺序是左中右,先访问的是二叉树顶部的节点,然后一层一层向下访问,直到到达树左面的最底部,再开始处理节点(也就是在把节点的数值放进result数组中)就造成了处理顺序和访问顺序是不一致的。
- 使用迭代法写中序遍历,就需要借用指针的遍历来帮助访问节点,栈则用来处理节点上的元素。
Inorder Binary Tree (Recursion)
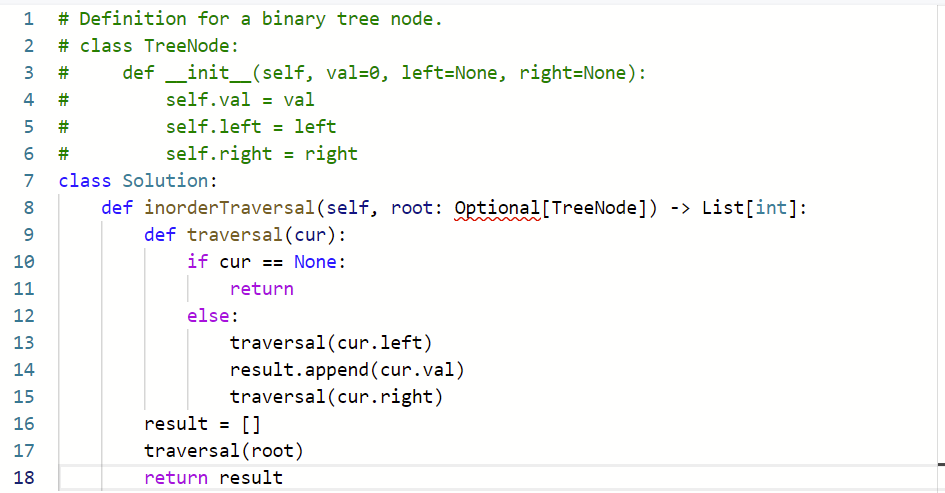
之后再考虑下N叉树的iteration
###
4.二叉树的改造和修改
226. 翻转二叉树
难度简单1177
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
示例 1:

输入:root = [4,2,7,1,3,6,9]
输出:[4,7,2,9,6,3,1]
示例 2:

输入:root = [2,1,3]
输出:[2,3,1]
示例 3:
输入:root = []
输出:[]
思路:
- 本质就是每个节点下面的两个换一下位置,所以很容易想到迭代法
- 先转换root下面的两个节点,再把这两个节点当作root进行迭代
- 迭代法就是把这些node存储在一个东西里面
代码:
- 递归法(前序遍历)
- 使用前序遍历,就是中左右
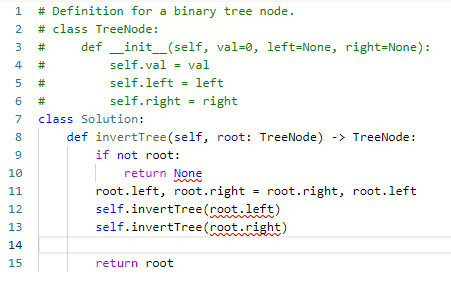
- 所有的节点只会被访问一次,所以时间复杂度是O(n),
- Because of recursion, O(h) function calls will be placed on the stack for the worst case, h is the height of the tree, so space complexity should also be O(n)
- 迭代法
- 使用迭代法就是BFS,深度优先搜索
- 想到BFS,和迭代,层序遍历,常用的数据结构就是deque,双向队列

106. 从中序与后序遍历序列构造二叉树
难度中等675
给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
示例 1:

输入:inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出:[3,9,20,null,null,15,7]
示例 2:
输入:inorder = [-1], postorder = [-1]
输出:[-1]
思路:
- 首先,后序遍历最后的一个一定是根节点,然后中序遍历找到根节点就是把它分为了左右两个部分
- 左边部分即左子树,右边部分为右子树,针对每个部分可以用同样的方法继续递归下去构造。
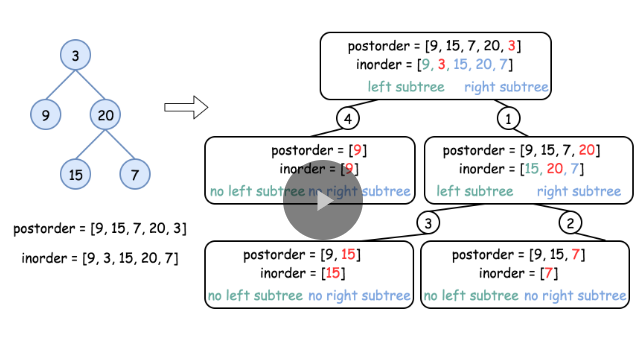
- 记住,创建树是用的inorder,分割树是用postorder

代码:
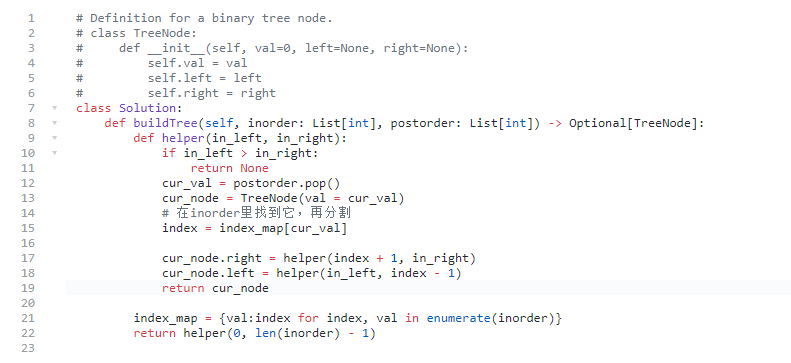
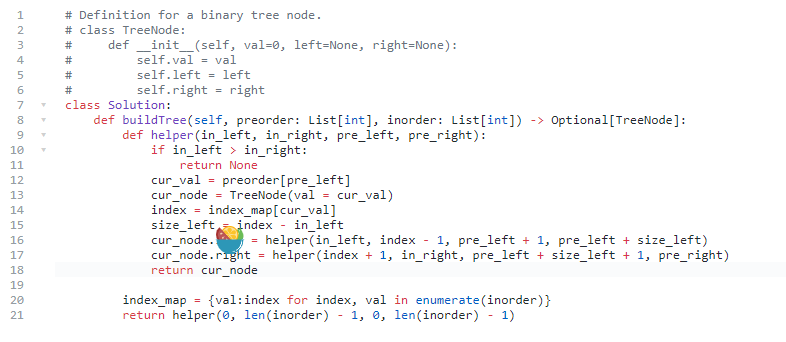
105. 从前序与中序遍历序列构造二叉树
难度中等1432
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
示例 1:

输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]
示例 2:
输入: preorder = [-1], inorder = [-1]
输出: [-1]
思路:
注意,中序和前序都去掉了root,且通过中序可以找到左树和右树的大小,就可以分割出左右树的前序和中序
代码:
654. 最大二叉树
难度中等372
给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:
- 创建一个根节点,其值为
nums中的最大值。 - 递归地在最大值 左边 的 子数组前缀上 构建左子树。
- 递归地在最大值 右边 的 子数组后缀上 构建右子树。
返回 nums 构建的 *最大二叉树* 。
示例 1:

输入:nums = [3,2,1,6,0,5]
输出:[6,3,5,null,2,0,null,null,1]
解释:递归调用如下所示:
- [3,2,1,6,0,5] 中的最大值是 6 ,左边部分是 [3,2,1] ,右边部分是 [0,5] 。
- [3,2,1] 中的最大值是 3 ,左边部分是 [] ,右边部分是 [2,1] 。
- 空数组,无子节点。
- [2,1] 中的最大值是 2 ,左边部分是 [] ,右边部分是 [1] 。
- 空数组,无子节点。
- 只有一个元素,所以子节点是一个值为 1 的节点。
- [0,5] 中的最大值是 5 ,左边部分是 [0] ,右边部分是 [] 。
- 只有一个元素,所以子节点是一个值为 0 的节点。
- 空数组,无子节点。
示例 2:

输入:nums = [3,2,1]
输出:[3,null,2,null,1]
思路:
- 递归法:
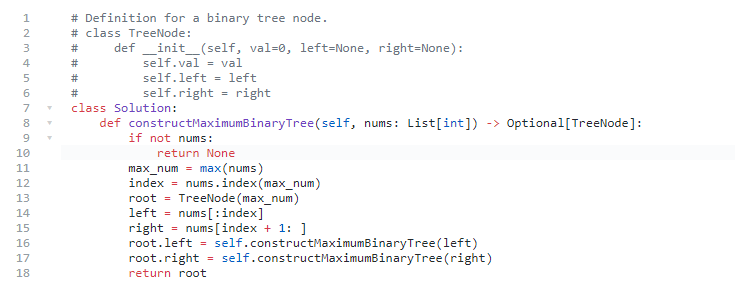
- 这道题实际上是使用单调栈进行的解决
- 现在带数字测试能理解它的正确性,但是还需要更多的练习
代码:
617. 合并二叉树
难度简单880
给你两棵二叉树: root1 和 root2 。
想象一下,当你将其中一棵覆盖到另一棵之上时,两棵树上的一些节点将会重叠(而另一些不会)。你需要将这两棵树合并成一棵新二叉树。合并的规则是:如果两个节点重叠,那么将这两个节点的值相加作为合并后节点的新值;否则,不为 null 的节点将直接作为新二叉树的节点。
返回合并后的二叉树。
注意: 合并过程必须从两个树的根节点开始。
示例 1:
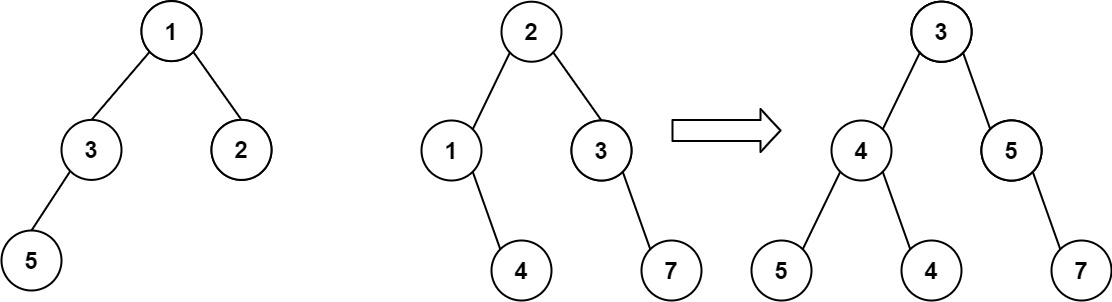
输入:root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
输出:[3,4,5,5,4,null,7]
示例 2:
输入:root1 = [1], root2 = [1,2]
输出:[2,2]
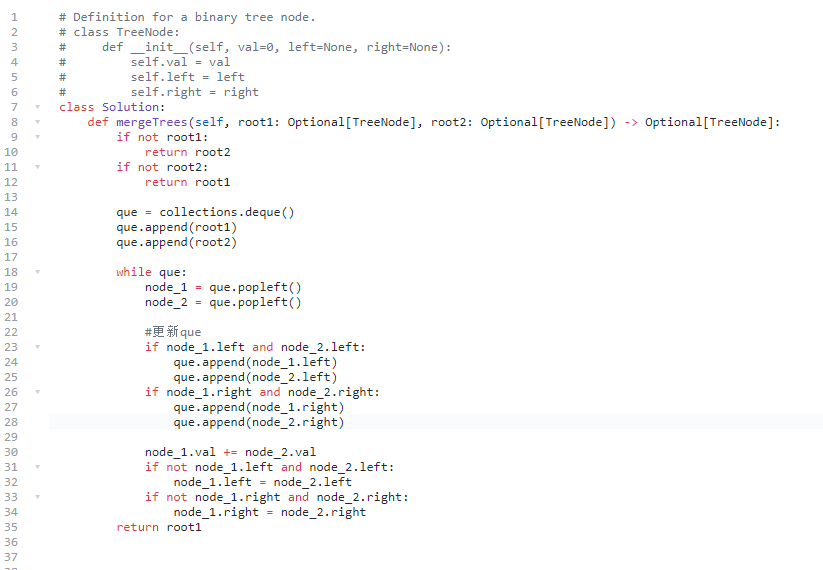
思路:
- 使用递归的方法,把两棵树都合并到root1上,这样没有新建节点,节省空间

- 使用迭代,求二叉树对称的计算结果时候就是把两个树的节点同时加入队列进行操作,类似于101题
536. 从字符串生成二叉树
难度中等83
你需要用一个包括括号和整数的字符串构建一棵二叉树。
输入的字符串代表一棵二叉树。它包括整数和随后的 0 、1 或 2 对括号。整数代表根的值,一对括号内表示同样结构的子树。
若存在子结点,则从左子结点开始构建。
示例 1:
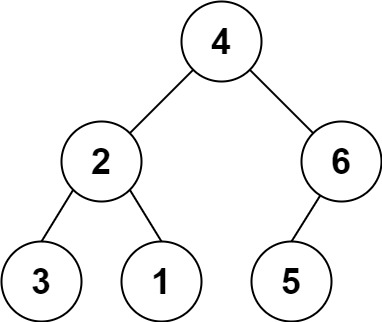
输入: s = "4(2(3)(1))(6(5))"
输出: [4,2,6,3,1,5]
示例 2:
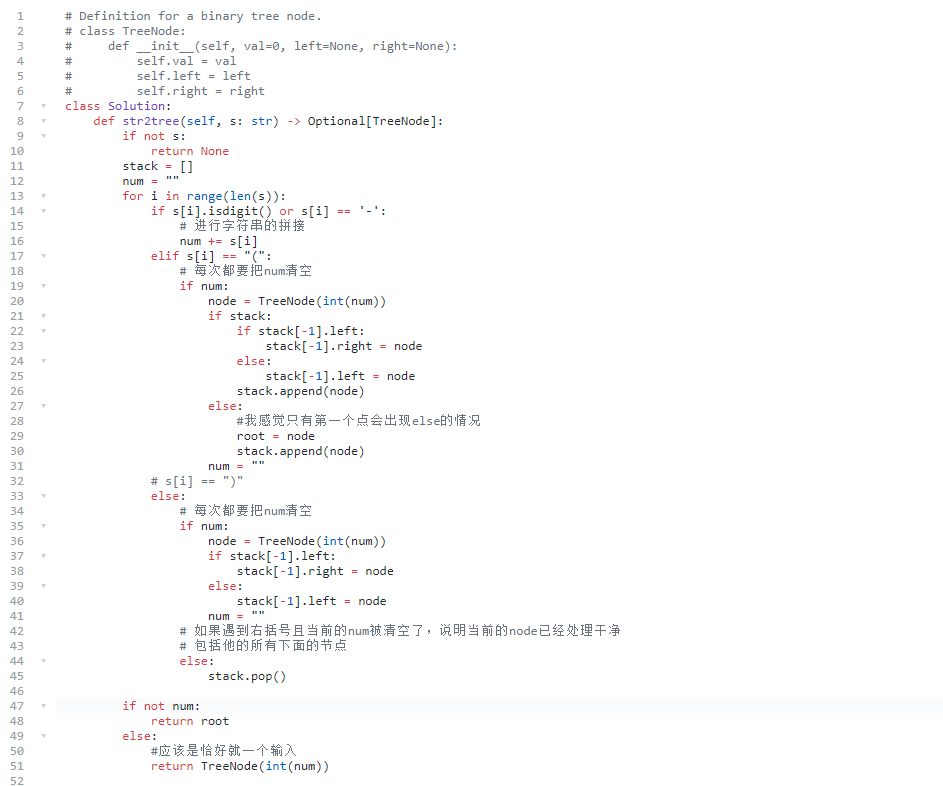
输入: s = "4(2(3)(1))(6(5)(7))"
输出: [4,2,6,3,1,5,7]
示例 3:
输入: s = "-4(2(3)(1))(6(5)(7))"
输出: [-4,2,6,3,1,5,7]
提示:
0 <= s.length <= 3 * 104- 输入字符串中只包含
'(',')','-'和'0'~'9' - 空树由
""而非"()"表示。
思路:
- If
s[i]is a digit or"-", we updatenumbynum += s[i]. - If
s[i] == "("andnumsnon-empty, we assignstack[-1].lefttonumsif it has not yet been assigned, else we assignstack[-1].righttonums. After this, we appendnumstostack. - If
s[i] == ")": (i). Ifnumsnonempty, we assignstack[-1].lefttonumsif it has not yet been assigned, else we assignstack[-1].righttonums. Contrary to the previous case, we do not appendnumsto stack. (ii). Ifnumsis empty, we dostack.pop()so thatstack[-1]becomes the parent of the popped node.
5.二叉搜索树的属性
二叉搜索树的定义
二叉搜索树是一个有序树:
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 它的左、右子树也分别为二叉搜索树
700. 二叉搜索树中的搜索
难度简单242
给定二叉搜索树(BST)的根节点 root 和一个整数值 val。
你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在,则返回 null 。
示例 1:
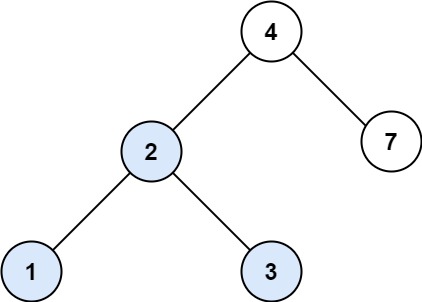
输入:root = [4,2,7,1,3], val = 2
输出:[2,1,3]
Example 2:
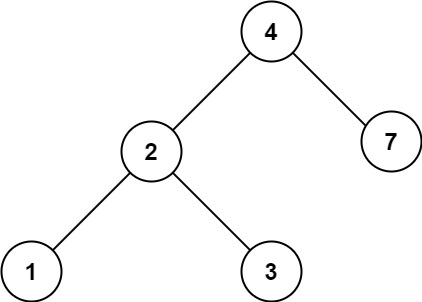
输入:root = [4,2,7,1,3], val = 5
输出:[]
思路:
recursion:
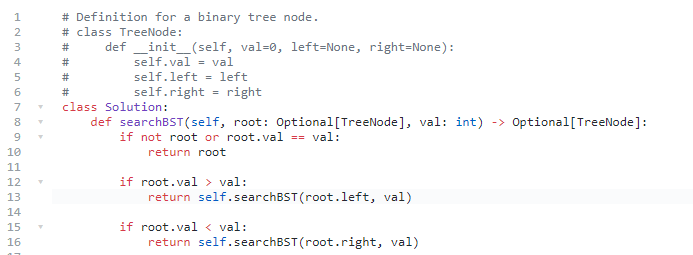
Iteration:
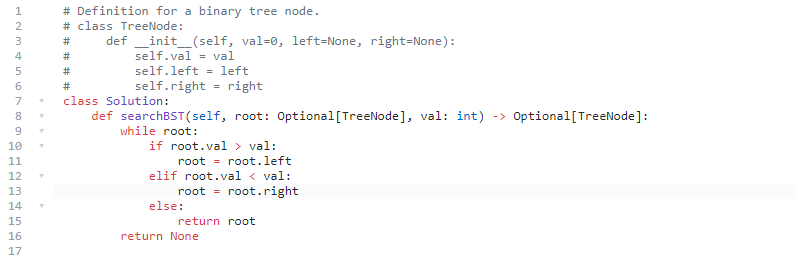
98. 验证二叉搜索树
难度中等1420
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
- 节点的左子树只包含 小于 当前节点的数。
- 节点的右子树只包含 大于 当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
示例 1:

输入:root = [2,1,3]
输出:true
示例 2:

输入:root = [5,1,4,null,null,3,6]
输出:false
解释:根节点的值是 5 ,但是右子节点的值是 4 。
思路:
使用math.inf来确定上下界,使用上下界来确定
Recursion:

Iteration:
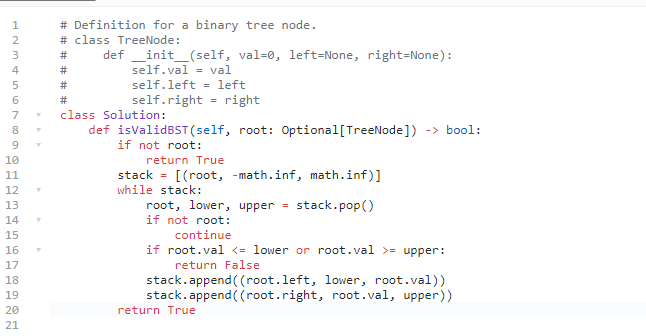
530. 二叉搜索树的最小绝对差
难度简单308
给你一个二叉搜索树的根节点 root ,返回 树中任意两不同节点值之间的最小差值 。
差值是一个正数,其数值等于两值之差的绝对值。
示例 1:

输入:root = [4,2,6,1,3]
输出:1
示例 2:

输入:root = [1,0,48,null,null,12,49]
输出:1
思路:
这道题很容易产生一个误解,就是相邻的node之间的差
但是实际上是所有的节点之间的差
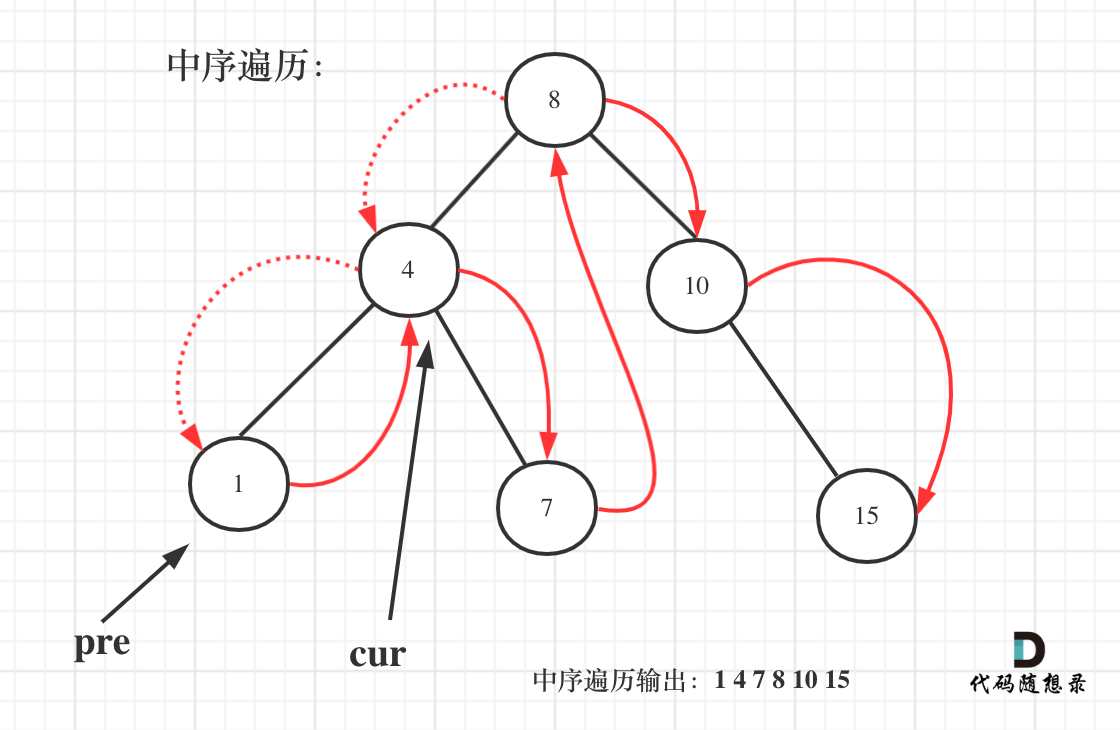
这里7是可以比4大的,他只要遵循大于4,小于8
501. 二叉搜索树中的众数
难度简单451
给你一个含重复值的二叉搜索树(BST)的根节点 root ,找出并返回 BST 中的所有 众数(即,出现频率最高的元素)。
如果树中有不止一个众数,可以按 任意顺序 返回。
假定 BST 满足如下定义:
- 结点左子树中所含节点的值 小于等于 当前节点的值
- 结点右子树中所含节点的值 大于等于 当前节点的值
- 左子树和右子树都是二叉搜索树
示例 1:
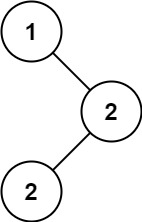
输入:root = [1,null,2,2]
输出:[2]
示例 2:
输入:root = [0]
输出:[0]
提示:
- 树中节点的数目在范围
[1, 104]内 -105 <= Node.val <= 105
进阶:你可以不使用额外的空间吗?(假设由递归产生的隐式调用栈的开销不被计算在内)
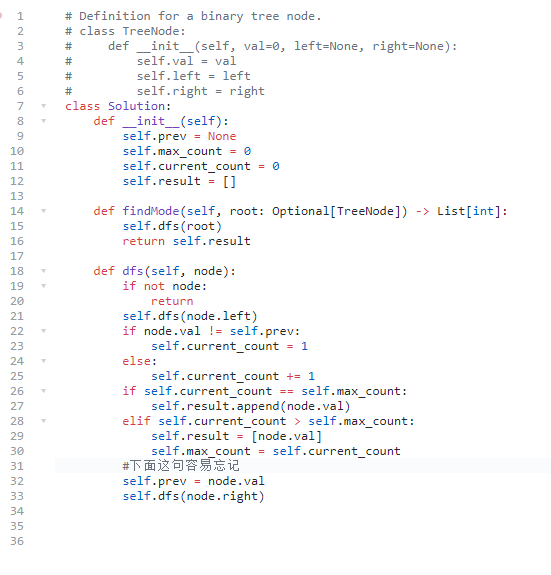
这道题的关键点在于Inorder traversal of a BST will find the nodes in ascending order.
也就是BST的中序遍历将以递增的顺序返回Tree的节点值
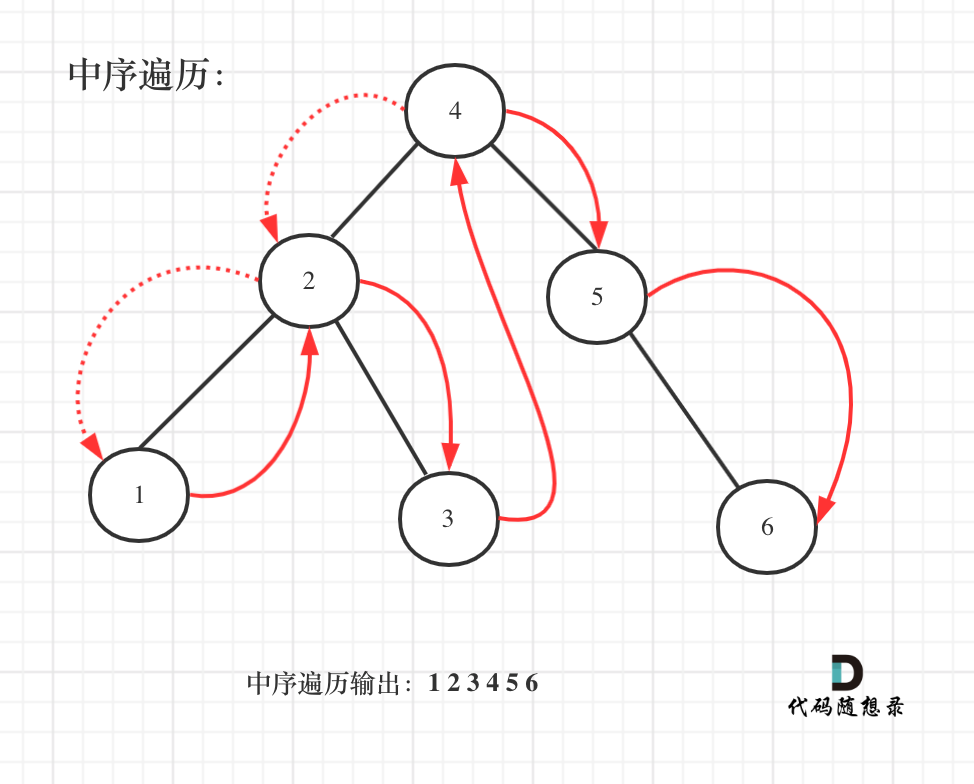
- So just compare the current node to the previous, and if they match, increase the current count of duplicate values by 1.
- If they don’t match, reset the current count to 1. Compare the current count to the max count found so far.
- If they match, append the current value to the result list.
- If the current count of duplicates exceeds the max count, create a new result list with just the current value.
538. 把二叉搜索树转换为累加树
难度中等713
给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
提醒一下,二叉搜索树满足下列约束条件:
- 节点的左子树仅包含键 小于 节点键的节点。
- 节点的右子树仅包含键 大于 节点键的节点。
- 左右子树也必须是二叉搜索树。
注意:本题和 1038: https://leetcode-cn.com/problems/binary-search-tree-to-greater-sum-tree/ 相同
示例 1:
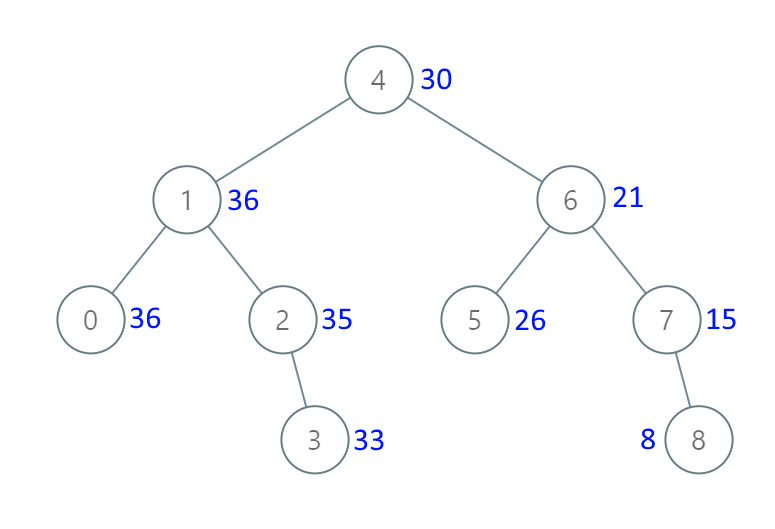
输入:[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出:[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
示例 2:
输入:root = [0,null,1]
输出:[1,null,1]
示例 3:
输入:root = [1,0,2]
输出:[3,3,2]
示例 4:
输入:root = [3,2,4,1]
输出:[7,9,4,10]
提示:
- 树中的节点数介于
0和104之间。 - 每个节点的值介于
-104和104之间。 - 树中的所有值 互不相同。
- 给定的树为二叉搜索树
6. 二叉树的公共祖先
235. 二叉搜索树的最近公共祖先
难度简单829
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

示例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。
说明:
- 所有节点的值都是唯一的。
- p、q 为不同节点且均存在于给定的二叉搜索树中。
236. 二叉树的最近公共祖先
难度中等1731
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例 1:

输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出:3
解释:节点 5 和节点 1 的最近公共祖先是节点 3 。
示例 2:

输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出:5
解释:节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。
示例 3:
输入:root = [1,2], p = 1, q = 2
输出:1
提示:
- 树中节点数目在范围
[2, 105]内。 -109 <= Node.val <= 109- 所有
Node.val互不相同。 p != qp和q均存在于给定的二叉树中。
7. 二叉搜索树的修改和构造
701. 二叉搜索树中的插入操作
难度中等304
给定二叉搜索树(BST)的根节点 root 和要插入树中的值 value ,将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ,新值和原始二叉搜索树中的任意节点值都不同。
注意,可能存在多种有效的插入方式,只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。
示例 1:
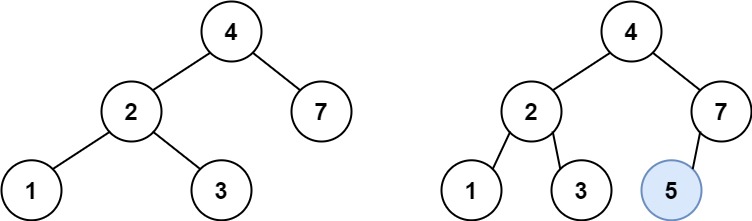
输入:root = [4,2,7,1,3], val = 5
输出:[4,2,7,1,3,5]
解释:另一个满足题目要求可以通过的树是:
示例 2:
输入:root = [40,20,60,10,30,50,70], val = 25
输出:[40,20,60,10,30,50,70,null,null,25]
示例 3:
输入:root = [4,2,7,1,3,null,null,null,null,null,null], val = 5
输出:[4,2,7,1,3,5]
提示:
- 树中的节点数将在
[0, 104]的范围内。 -108 <= Node.val <= 108- 所有值
Node.val是 独一无二 的。 -108 <= val <= 108- 保证
val在原始BST中不存在。
450. 删除二叉搜索树中的节点
难度中等738
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:
- 首先找到需要删除的节点;
- 如果找到了,删除它。
示例 1:
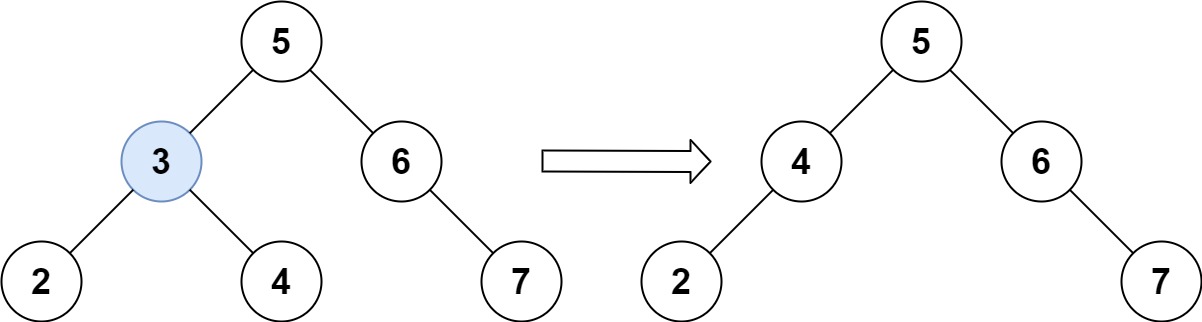
输入:root = [5,3,6,2,4,null,7], key = 3
输出:[5,4,6,2,null,null,7]
解释:给定需要删除的节点值是 3,所以我们首先找到 3 这个节点,然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。
示例 2:
输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点
示例 3:
输入: root = [], key = 0
输出: []
提示:
- 节点数的范围
[0, 104]. -105 <= Node.val <= 105- 节点值唯一
root是合法的二叉搜索树-105 <= key <= 105
进阶: 要求算法时间复杂度为 O(h),h 为树的高度。
776. 拆分二叉搜索树
难度中等109
给你一棵二叉搜索树(BST)的根结点 root 和一个整数 target 。请将该树按要求拆分为两个子树:其中一个子树结点的值都必须小于等于给定的目标值;另一个子树结点的值都必须大于目标值;树中并非一定要存在值为 target 的结点。
除此之外,树中大部分结构都需要保留,也就是说原始树中父节点 p 的任意子节点 c ,假如拆分后它们仍在同一个子树中,那么结点 p 应仍为 c 的父结点。
返回 两个子树的根结点的数组 。
示例 1:
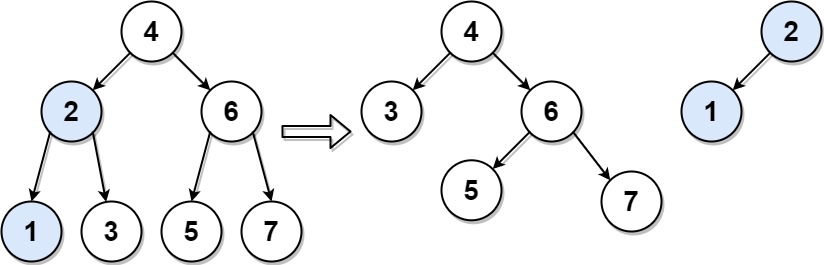
输入:root = [4,2,6,1,3,5,7], target = 2
输出:[[2,1],[4,3,6,null,null,5,7]]
示例 2:
输入: root = [1], target = 1
输出: [[1],[]]
提示:
- 二叉搜索树节点个数在
[1, 50]范围内 0 <= Node.val, target <= 1000
669. 修剪二叉搜索树
难度中等530
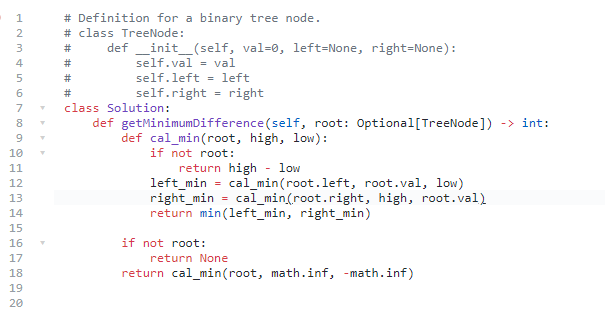
给你二叉搜索树的根节点 root ,同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树,使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即,如果没有被移除,原有的父代子代关系都应当保留)。 可以证明,存在 唯一的答案 。
所以结果应当返回修剪好的二叉搜索树的新的根节点。注意,根节点可能会根据给定的边界发生改变。
示例 1:
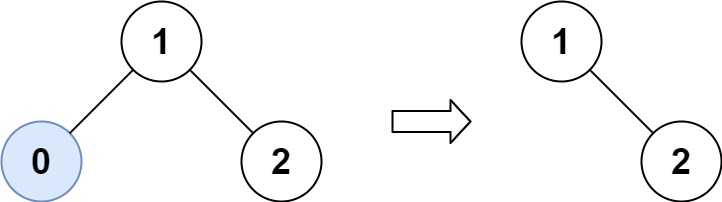
输入:root = [1,0,2], low = 1, high = 2
输出:[1,null,2]
示例 2:
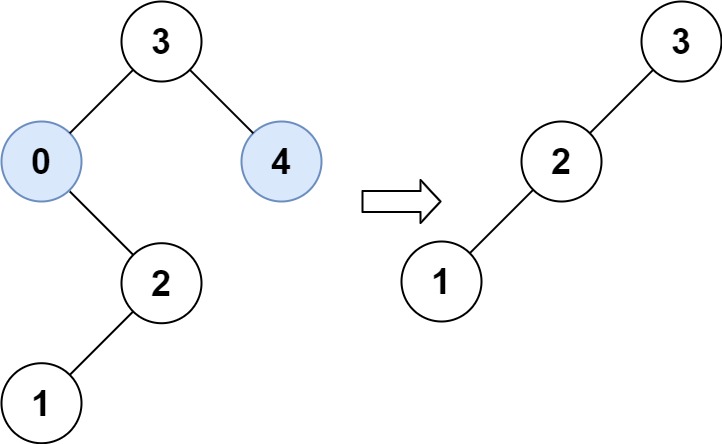
输入:root = [3,0,4,null,2,null,null,1], low = 1, high = 3
输出:[3,2,null,1]
提示:
- 树中节点数在范围
[1, 104]内 0 <= Node.val <= 104- 树中每个节点的值都是 唯一 的
- 题目数据保证输入是一棵有效的二叉搜索树
0 <= low <= high <= 104
108. 将有序数组转换为二叉搜索树
难度简单1030
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 高度平衡 二叉搜索树。
高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。
示例 1:
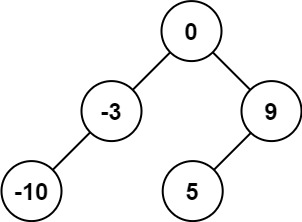
输入:nums = [-10,-3,0,5,9]
输出:[0,-3,9,-10,null,5]
解释:[0,-10,5,null,-3,null,9] 也将被视为正确答案:
示例 2:
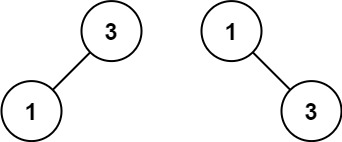
输入:nums = [1,3]
输出:[3,1]
解释:[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。
提示:
1 <= nums.length <= 104-104 <= nums[i] <= 104nums按 严格递增 顺序排列
235. Lowest Common Ancestor of a Binary Search Tree
难度简单822
Given a binary search tree (BST), find the lowest common ancestor (LCA) of two given nodes in the BST.
According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”
Example 1:
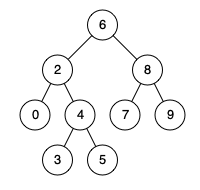
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
Output: 6
Explanation: The LCA of nodes 2 and 8 is 6.
Example 2:

Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
Output: 2
Explanation: The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.
Example 3:
Input: root = [2,1], p = 2, q = 1
Output: 2
Constraints:
- The number of nodes in the tree is in the range
[2, 105]. -109 <= Node.val <= 109- All
Node.valare unique. p != qpandqwill exist in the BST.
思路:
注意二叉搜索树的特点是左边比中间小,右边比中间大
二叉树不是这样的,两边是什么都可以
如果采用递归的方法:
- 从根节点开始遍历树。
- 如果两个节点
p和q都在右子树中,则从步骤 1 开始以右子树继续搜索。 - 如果两个节点
p都q在左子树中,则从第 1 步开始从左子树继续搜索。 - 如果第 2 步和第 3 步都不为真,这意味着我们找到了 node
p和q的子树共有的节点。因此我们将这个公共节点作为 LCA 返回。 - Time Complexity: O(N)O(N), where NN is the number of nodes in the BST. In the worst case we might be visiting all the nodes of the BST.
- Space Complexity: O(N)O(N). This is because the maximum amount of space utilized by the recursion stack would be NN since the height of a skewed BST could be NN.
代码:
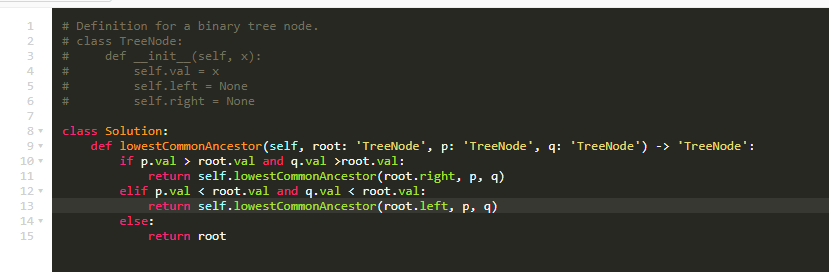
- 注意递归要return和self
236. Lowest Common Ancestor of a Binary Tree
难度中等1704
Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree.
According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”
Example 1:

Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
Output: 3
Explanation: The LCA of nodes 5 and 1 is 3.
Example 2:

Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
Output: 5
Explanation: The LCA of nodes 5 and 4 is 5, since a node can be a descendant of itself according to the LCA definition.
Example 3:
Input: root = [1,2], p = 1, q = 2
Output: 1
Constraints:
- The number of nodes in the tree is in the range
[2, 105]. -109 <= Node.val <= 109- All
Node.valare unique. p != qpandqwill exist in the tree.
思路
- 这题不再是二叉搜索树,而是二叉树

dfs从根向下到它的子节点,如果是troot == p或root == qthen root`必须是它们的LCA。- 如果
left子树包含后代(p或q)之一,而right子树包含剩余的后代(q或p),则root是它们的 LCA。 - 如果
left子树同时包含两者p,q则left作为它们的 LCA 返回。 - 如果
right子树同时包含两者p,q则right作为它们的 LCA 返回。
代码
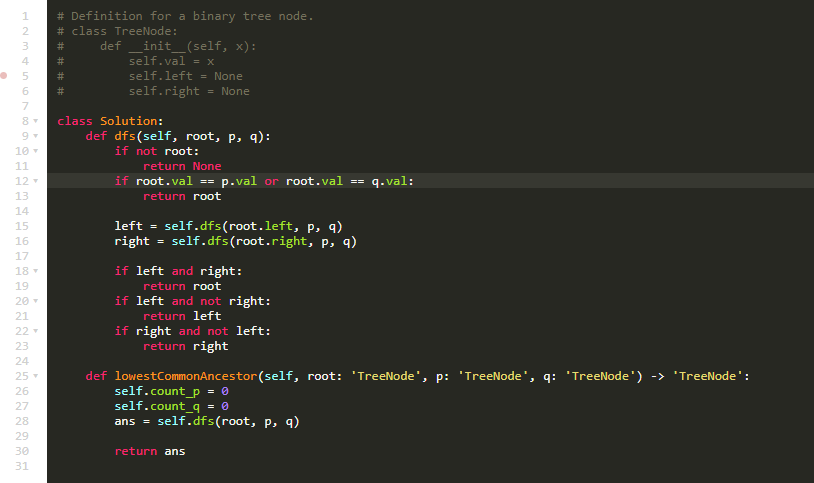
314. Binary Tree Vertical Order Traversal
难度中等165
Given the root of a binary tree, return the vertical order traversal of its nodes’ values. (i.e., from top to bottom, column by column).
If two nodes are in the same row and column, the order should be from left to right.
Example 1:
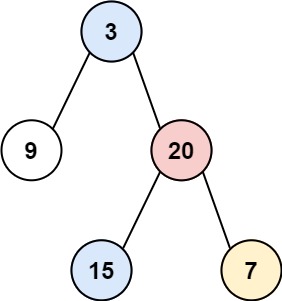
Input: root = [3,9,20,null,null,15,7]
Output: [[9],[3,15],[20],[7]]
Example 2:
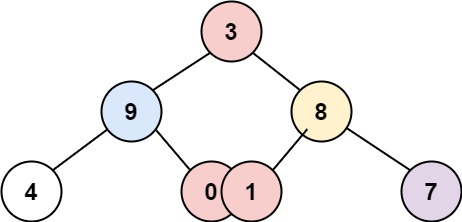
Input: root = [3,9,8,4,0,1,7]
Output: [[4],[9],[3,0,1],[8],[7]]
Example 3:
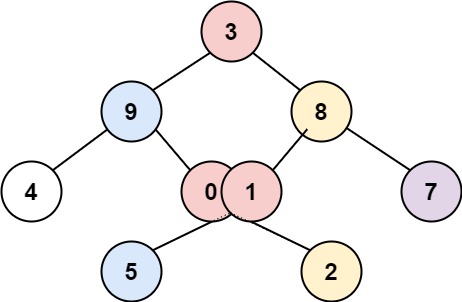
Input: root = [3,9,8,4,0,1,7,null,null,null,2,5]
Output: [[4],[9,5],[3,0,1],[8,2],[7]]
Constraints:
- The number of nodes in the tree is in the range
[0, 100]. -100 <= Node.val <= 100
思路:
- 通过题目描述,最直观的方法是BFS,我们希望维护一个哈希表,key would be the column, and value would be a list which contains the values of nodes in the same column
- For BFS, we often use a queue to keep track of the order to visit the nodes.
- At each iteration within the BFS, we pop out an element from the queue. And it should tell us column index and node value
- Then we put its children nodes into column - 1 and column + 1
- In the end, we sort the hash table by its key: column index

Complexity Analysis
- Time Complexity: O(nlgn) For BFS traversal, we traversed each node once and only once, O(n) We sorted the hash table by its keys. It should be O(nlgn), if the binary tree is extremely imbalanced, it would be O(nlgn)
- Space Complexity: O(n) Hash Table: O(n) During the BFS traversal, we use a queue to keep track of the next node to visit. For binary tree, the max number of nodes would be (N+1)/2, which is also the number of leafs in a full binary tree. SO it should be O(n)
代码:
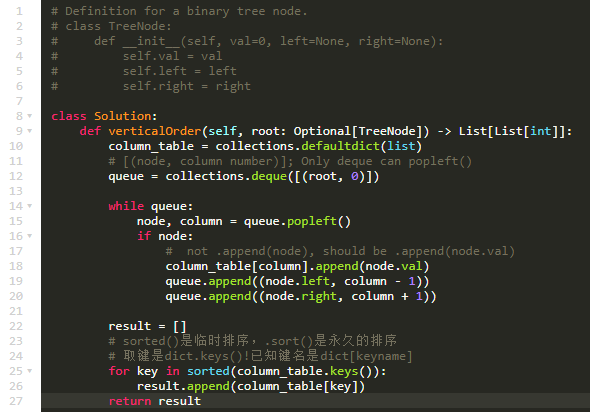
Improve:
思路:
- we can simply iterate to generate the outputs without need for sorting
- During the BFS, we can know the range of column indeices
- At the end of BFS traversal, we would walk though [min_column, max_column] and find the results
- Time and space complexity should be O(n)
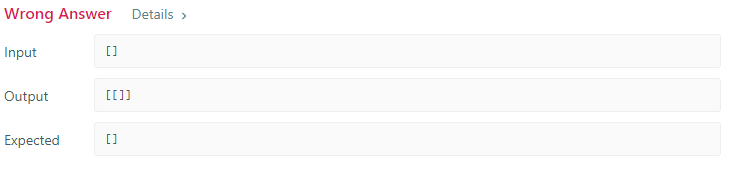
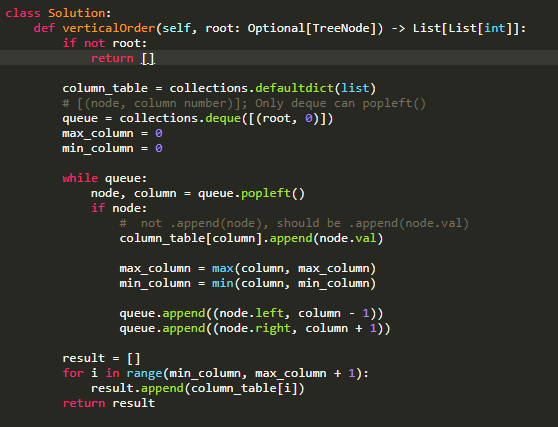
代码:
- 注意要对特殊情况,空输入进行判断,否则会报错,面试一定要注意
1644. Lowest Common Ancestor of a Binary Tree II
难度中等24
Given the root of a binary tree, return the lowest common ancestor (LCA) of two given nodes, p and q. If either node p or q does not exist in the tree, return null. All values of the nodes in the tree are unique.
According to the definition of LCA on Wikipedia: “The lowest common ancestor of two nodes p and q in a binary tree T is the lowest node that has both p and q as descendants (where we allow a node to be a descendant of itself)”. A descendant of a node x is a node y that is on the path from node x to some leaf node.
Example 1:

Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
Output: 3
Explanation: The LCA of nodes 5 and 1 is 3.
Example 2:

Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
Output: 5
Explanation: The LCA of nodes 5 and 4 is 5. A node can be a descendant of itself according to the definition of LCA.
Example 3:

Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 10
Output: null
Explanation: Node 10 does not exist in the tree, so return null.
Constraints:
- The number of nodes in the tree is in the range
[1, 104]. -109 <= Node.val <= 109- All
Node.valare unique. p != q
Follow up: Can you find the LCA traversing the tree, without checking nodes existence?
思路:
- 这道题和上一题的区别在于p和q不一定存在于tree中,相比起上一题需要记录是否找到p和q
- 注意这里面对于root和p,q的判断应该发生在对 children 的递归调用之后。因为我们需要遍历所有节点。
- 这是和236不同的地方
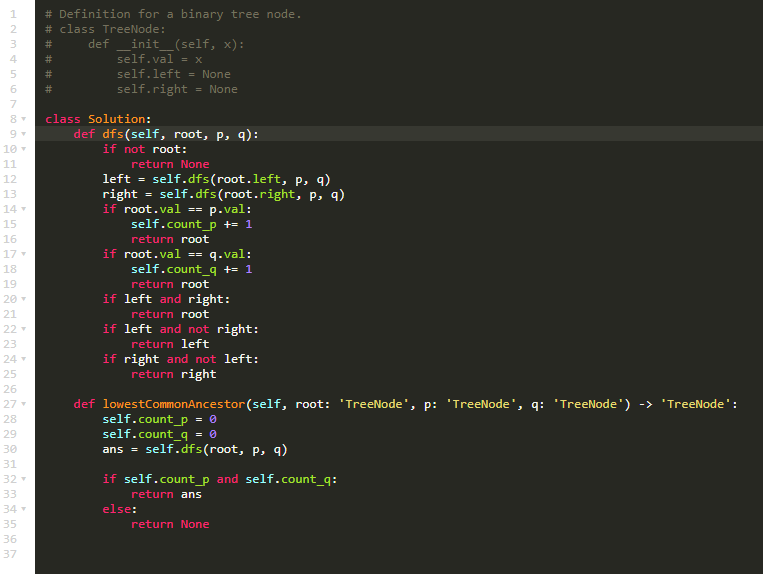
代码:
1650. Lowest Common Ancestor of a Binary Tree III
难度中等27
Given two nodes of a binary tree p and q, return their lowest common ancestor (LCA).
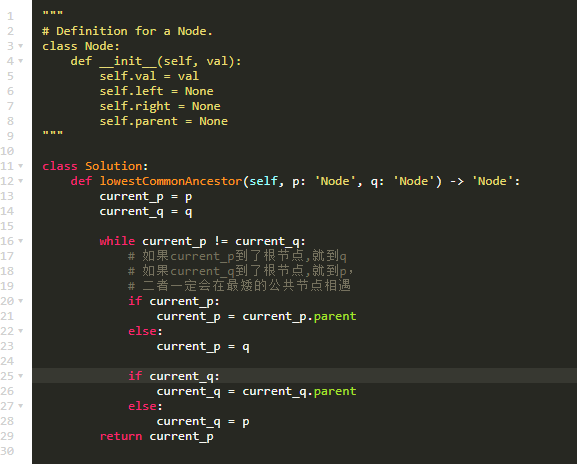
Each node will have a reference to its parent node. The definition for Node is below:
class Node {
public int val;
public Node left;
public Node right;
public Node parent;
}
According to the definition of LCA on Wikipedia: “The lowest common ancestor of two nodes p and q in a tree T is the lowest node that has both p and q as descendants (where we allow a node to be a descendant of itself).”
Example 1:
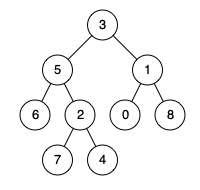
Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
Output: 3
Explanation: The LCA of nodes 5 and 1 is 3.
Example 2:

Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
Output: 5
Explanation: The LCA of nodes 5 and 4 is 5 since a node can be a descendant of itself according to the LCA definition.
Example 3:
Input: root = [1,2], p = 1, q = 2
Output: 1
Constraints:
- The number of nodes in the tree is in the range
[2, 105]. -109 <= Node.val <= 109- All
Node.valare unique. p != qpandqexist in the tree.
思路:
- 因为可以找parent,所以可以p和q同时网上面找
- 如果使用哈希表面试会失败。应该在 O(1) 空间中求解。用哈希表(查找时间复杂度为O(1))记录已经走过的结点,重合的结点即为答案
- 此题去除其他节点,只看从给定的两个节点到根节点路径上的所有节点,则其可等效为双链表的交点问题
- 设两个指针分别从两个给定节点出发,如果两个节点不等,则继续往前一步。如果某个节点到达根节点,则跳到另一个给定的节点。最终两个指针一定会相遇在交点处,因为到交点处的路径上面指针走过的路程为L1 + L3 + L2,下面的指针走过的路程为L2 + L3 + L1
- 这道题和160题链表相交的思路一样
代码:
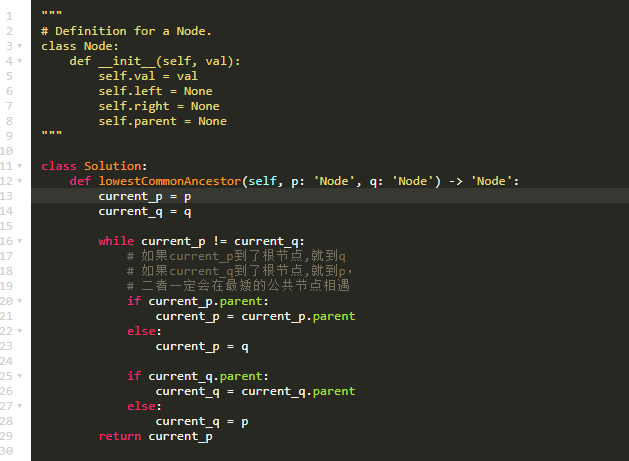
判断的时候删掉parent也可以,不知道为什么160不行