Binary Search Exercise 2

33. Search in Rotated Sorted Array

难度中等2069

There is an integer array nums sorted in ascending order (with distinct values).

Prior to being passed to your function, nums is possibly rotated at an unknown pivot index k (1 <= k < nums.length) such that the resulting array is [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]] (0-indexed). For example, [0,1,2,4,5,6,7] might be rotated at pivot index 3 and become [4,5,6,7,0,1,2].

Given the array nums after the possible rotation and an integer target, return the index of target if it is in nums, or -1 if it is not in nums.

You must write an algorithm with O(log n) runtime complexity.

Example 1:

Input: nums = [4,5,6,7,0,1,2], target = 0
Output: 4

Example 2:

Input: nums = [4,5,6,7,0,1,2], target = 3
Output: -1

Example 3:

Input: nums = [1], target = 0
Output: -1

Constraints:

1 <= nums.length <= 5000
-104 <= nums[i] <= 104
All values of nums are unique.
nums is an ascending array that is possibly rotated.
-104 <= target <= 104

4. Median of Two Sorted Arrays

难度困难5419

Given two sorted arrays nums1 and nums2 of size m and n respectively, return the median of the two sorted arrays.

The overall run time complexity should be O(log (m+n)).

Example 1:

Input: nums1 = [1,3], nums2 = [2]
Output: 2.00000
Explanation: merged array = [1,2,3] and median is 2.

Example 2:

Input: nums1 = [1,2], nums2 = [3,4]
Output: 2.50000
Explanation: merged array = [1,2,3,4] and median is (2 + 3) / 2 = 2.5.

Constraints:

nums1.length == m
nums2.length == n
0 <= m <= 1000
0 <= n <= 1000
1 <= m + n <= 2000
-106 <= nums1[i], nums2[i] <= 106

1235. Maximum Profit in Job Scheduling

难度困难152

We have n jobs, where every job is scheduled to be done from startTime[i] to endTime[i], obtaining a profit of profit[i].

You’re given the startTime, endTime and profit arrays, return the maximum profit you can take such that there are no two jobs in the subset with overlapping time range.

If you choose a job that ends at time X you will be able to start another job that starts at time X.

Example 1:

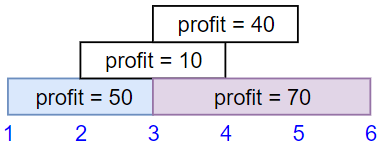
Input: startTime = [1,2,3,3], endTime = [3,4,5,6], profit = [50,10,40,70]
Output: 120
Explanation: The subset chosen is the first and fourth job. 
Time range [1-3]+[3-6] , we get profit of 120 = 50 + 70.

Example 2:

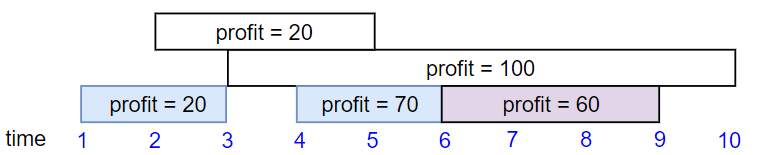
Input: startTime = [1,2,3,4,6], endTime = [3,5,10,6,9], profit = [20,20,100,70,60]
Output: 150
Explanation: The subset chosen is the first, fourth and fifth job. 
Profit obtained 150 = 20 + 70 + 60.

Example 3:

Input: startTime = [1,1,1], endTime = [2,3,4], profit = [5,6,4]
Output: 6

Constraints:

1 <= startTime.length == endTime.length == profit.length <= 5 * 104
1 <= startTime[i] < endTime[i] <= 109
1 <= profit[i] <= 104

528. Random Pick with Weight

难度中等235

You are given a 0-indexed array of positive integers w where w[i] describes the weight of the ith index.

You need to implement the function pickIndex(), which randomly picks an index in the range [0, w.length - 1] (inclusive) and returns it. The probability of picking an index i is w[i] / sum(w).

For example, if w = [1, 3], the probability of picking index 0 is 1 / (1 + 3) = 0.25 (i.e., 25%), and the probability of picking index 1 is 3 / (1 + 3) = 0.75 (i.e., 75%).

Example 1:

Input
["Solution","pickIndex"]
[[[1]],[]]
Output
[null,0]

Explanation
Solution solution = new Solution([1]);
solution.pickIndex(); // return 0. The only option is to return 0 since there is only one element in w.

Example 2:

Input
["Solution","pickIndex","pickIndex","pickIndex","pickIndex","pickIndex"]
[[[1,3]],[],[],[],[],[]]
Output
[null,1,1,1,1,0]

Explanation
Solution solution = new Solution([1, 3]);
solution.pickIndex(); // return 1. It is returning the second element (index = 1) that has a probability of 3/4.
solution.pickIndex(); // return 1
solution.pickIndex(); // return 1
solution.pickIndex(); // return 1
solution.pickIndex(); // return 0. It is returning the first element (index = 0) that has a probability of 1/4.

Since this is a randomization problem, multiple answers are allowed.
All of the following outputs can be considered correct:
[null,1,1,1,1,0]
[null,1,1,1,1,1]
[null,1,1,1,0,0]
[null,1,1,1,0,1]
[null,1,0,1,0,0]
......
and so on.

Constraints:

1 <= w.length <= 104
1 <= w[i] <= 105
pickIndex will be called at most 104 times.

410. Split Array Largest Sum

难度困难681

Given an array nums which consists of non-negative integers and an integer m, you can split the array into m non-empty continuous subarrays.

Write an algorithm to minimize the largest sum among these m subarrays.

Example 1:

Input: nums = [7,2,5,10,8], m = 2
Output: 18
Explanation:
There are four ways to split nums into two subarrays.
The best way is to split it into [7,2,5] and [10,8],
where the largest sum among the two subarrays is only 18.

Example 2:

Input: nums = [1,2,3,4,5], m = 2
Output: 9

Example 3:

Input: nums = [1,4,4], m = 3
Output: 4

Constraints:

1 <= nums.length <= 1000
0 <= nums[i] <= 106
1 <= m <= min(50, nums.length)

1004. Max Consecutive Ones III

难度中等418

Given a binary array nums and an integer k, return the maximum number of consecutive 1’s in the array if you can flip at most k 0’s.

Example 1:

Input: nums = [1,1,1,0,0,0,1,1,1,1,0], k = 2
Output: 6
Explanation: [1,1,1,0,0,1,1,1,1,1,1]
Bolded numbers were flipped from 0 to 1. The longest subarray is underlined.

Example 2:

Input: nums = [0,0,1,1,0,0,1,1,1,0,1,1,0,0,0,1,1,1,1], k = 3
Output: 10
Explanation: [0,0,1,1,1,1,1,1,1,1,1,1,0,0,0,1,1,1,1]
Bolded numbers were flipped from 0 to 1. The longest subarray is underlined.

Constraints:

1 <= nums.length <= 105
nums[i] is either 0 or 1.
0 <= k <= nums.length

362. Design Hit Counter

难度中等81

Design a hit counter which counts the number of hits received in the past 5 minutes (i.e., the past 300 seconds).

Your system should accept a timestamp parameter (in seconds granularity), and you may assume that calls are being made to the system in chronological order (i.e., timestamp is monotonically increasing). Several hits may arrive roughly at the same time.

Implement the HitCounter class:

HitCounter() Initializes the object of the hit counter system.
void hit(int timestamp) Records a hit that happened at timestamp (in seconds). Several hits may happen at the same timestamp.
int getHits(int timestamp) Returns the number of hits in the past 5 minutes from timestamp (i.e., the past 300 seconds).

Example 1:

Input
["HitCounter", "hit", "hit", "hit", "getHits", "hit", "getHits", "getHits"]
[[], [1], [2], [3], [4], [300], [300], [301]]
Output
[null, null, null, null, 3, null, 4, 3]

Explanation
HitCounter hitCounter = new HitCounter();
hitCounter.hit(1);       // hit at timestamp 1.
hitCounter.hit(2);       // hit at timestamp 2.
hitCounter.hit(3);       // hit at timestamp 3.
hitCounter.getHits(4);   // get hits at timestamp 4, return 3.
hitCounter.hit(300);     // hit at timestamp 300.
hitCounter.getHits(300); // get hits at timestamp 300, return 4.
hitCounter.getHits(301); // get hits at timestamp 301, return 3.

Constraints:

1 <= timestamp <= 2 * 109
All the calls are being made to the system in chronological order (i.e., timestamp is monotonically increasing).
At most 300 calls will be made to hit and getHits.

Follow up: What if the number of hits per second could be huge? Does your design scale?

74. 搜索二维矩阵

难度中等637

编写一个高效的算法来判断 m x n 矩阵中，是否存在一个目标值。该矩阵具有如下特性：

每行中的整数从左到右按升序排列。
每行的第一个整数大于前一行的最后一个整数。

示例 1：

输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出：true

示例 2：

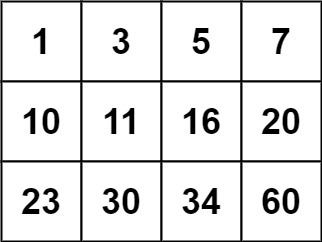
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
输出：false

提示：

m == matrix.length
n == matrix[i].length
1 <= m, n <= 100
-104 <= matrix[i][j], target <= 104

Binary Search Exercise 2