Graph Exercise 1
图的深度优先搜索:
深度优先遍历有「回头」的过程,在树中由于不存在「环」(回路),对于每一个结点来说,每一个结点只会被递归处理一次。而「图」中由于存在「环」(回路),就需要 记录已经被递归处理的结点(通常使用布尔数组或者哈希表),以免结点被重复遍历到。
图的广度优先遍历:
- 在 无权图 中,由于广度优先遍历本身的特点,假设源点为 source,只有在遍历到 所有 距离源点 source 的距离为 d 的所有结点以后,才能遍历到所有 距离源点 source 的距离为 d + 1 的所有结点。也可以使用「两点之间、线段最短」这条经验来辅助理解如下结论:从源点 source 到目标结点 target 走直线走过的路径一定是最短的。
- 和深度优先遍历一样,广度优先遍历也需要在遍历的时候记录已经遍历过的结点。
- 特别注意:将结点添加到队列以后,一定要马上标记为「已经访问」,否则相同结点会重复入队,这一点在初学的时候很容易忽略。如果很难理解这样做的必要性,建议大家在代码中打印出队列中的元素进行调试:在图中,如果入队的时候不马上标记为「已访问」,相同的结点会重复入队
-
广度优先遍历用于求解「无权图」的最短路径,因此一定要认清「无权图」这个前提条件。如果是带权图,就需要使用相应的专门的算法去解决它们。事实上,这些「专门」的算法的思想也都基于「广度优先遍历」的思想
- 带权有向图、且所有权重都非负的单源最短路径问题:使用 Dijkstra 算法;
- 带权有向图的单源最短路径问题:Bellman-Ford 算法;
- 一个图的所有结点对的最短路径问题:Floy-Warshall 算法。
- 应用任何一种算法,都需要认清使用算法的前提,不满足前提直接套用算法是不可取的。深刻理解应用算法的前提,也是学习算法的重要方法。例如我们在学习「二分查找」算法、「滑动窗口」算法的时候,就可以问自己,这个问题为什么可以使用「二分查找」,为什么可以使用「滑动窗口」。我们知道一个问题可以使用「优先队列」解决,是什么样的需求促使我们想到使用「优先队列」,而不是「红黑树(平衡二叉搜索树)」,想清楚使用算法(数据结构)的前提更重要。
Disjoint Set(查并集)
323. Number of Connected Components in an Undirected Graph
难度中等131
You have a graph of n nodes. You are given an integer n and an array edges where edges[i] = [ai, bi] indicates that there is an edge between ai and bi in the graph.
Return the number of connected components in the graph.
Example 1:
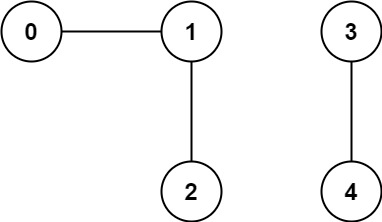
Input: n = 5, edges = [[0,1],[1,2],[3,4]]
Output: 2
Example 2:
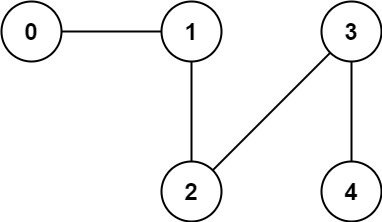
Input: n = 5, edges = [[0,1],[1,2],[2,3],[3,4]]
Output: 1
Constraints:
1 <= n <= 20001 <= edges.length <= 5000edges[i].length == 20 <= ai <= bi < nai != bi- There are no repeated edges.
思路:
- 首先需要对输入数组进行处理,由于 n 个结点的编号从 0 到 n - 1 ,因此可以使用「嵌套数组」表示邻接表 然后遍历每一个顶点,对每一个顶点执行一次广度优先遍历,注意:在遍历的过程中使用 visited 布尔数组记录已经遍历过的结点。
- 注意defaultdict(list)维护的dict用list作为值
- 这个部分会不断递归
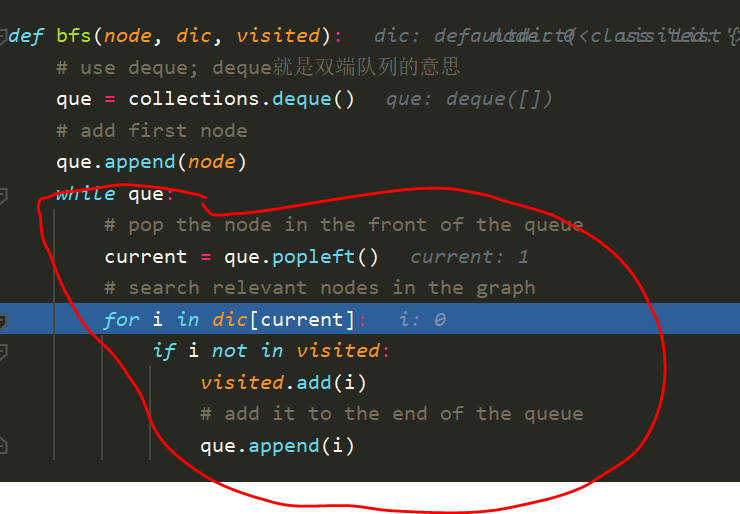
- 比如我们一开始看到的que是[0], 在popleft了0后, 它在搜索后发现1是连着的,就会加上1,变成[1];
- 再popleft了1后发现2是连着的,就会加上2,变成2。
- 2会看2连什么,2连的是1,1已经visited了,所以就没了,但是这时候visited是[0,1,2]
- 然后回到第一的函数,找每visited的点
代码:

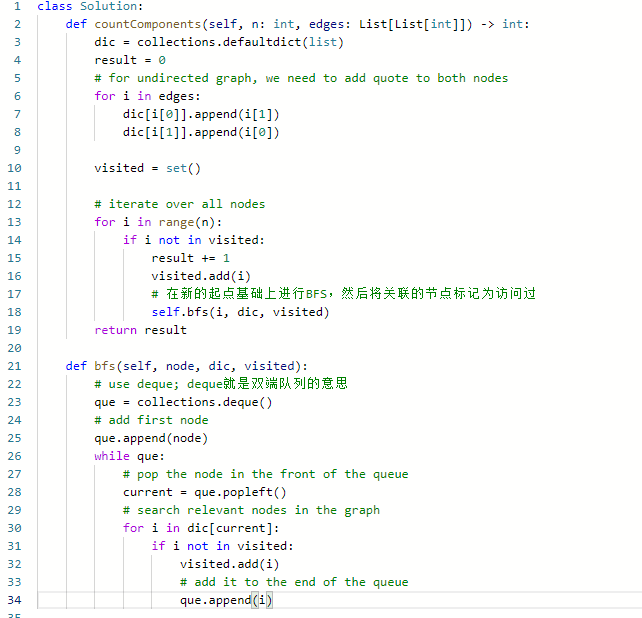
- 广度优先遍历可以用于「树」和「图」的问题的遍历;
- 广度优先遍历作用于「无权图」,得到的是「最短路径」。如果题目有让求「最小」、「最短」、「最少」,可以考虑这个问题是不是可以建立成一个「图形结构」或者「树形结构」,用「广度优先遍历」的思想求得「最小」、「最短」、「最少」的数值;
- 广度优先遍历作用于图论问题的时候,结点在加入队列以后标记为已经访问,否则会出现结点重复入队的情况。
###
79. Word Search
难度中等1259
Given an m x n grid of characters board and a string word, return true if word exists in the grid.
The word can be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once.
Example 1:
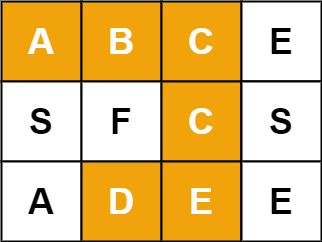
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
Output: true
Example 2:
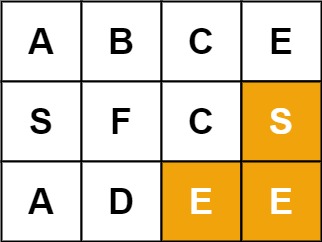
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
Output: true
Example 3:

Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
Output: false
Constraints:
m == board.lengthn = board[i].length1 <= m, n <= 61 <= word.length <= 15boardandwordconsists of only lowercase and uppercase English letters.
Follow up: Could you use search pruning to make your solution faster with a larger board?
思路:
代码:
695. 岛屿的最大面积
给你一个大小为 m x n 的二进制矩阵 grid 。
岛屿 是由一些相邻的 1 (代表土地) 构成的组合,这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0(代表水)包围着。
岛屿的面积是岛上值为 1 的单元格的数目。
计算并返回 grid 中最大的岛屿面积。如果没有岛屿,则返回面积为 0 。
示例 1:
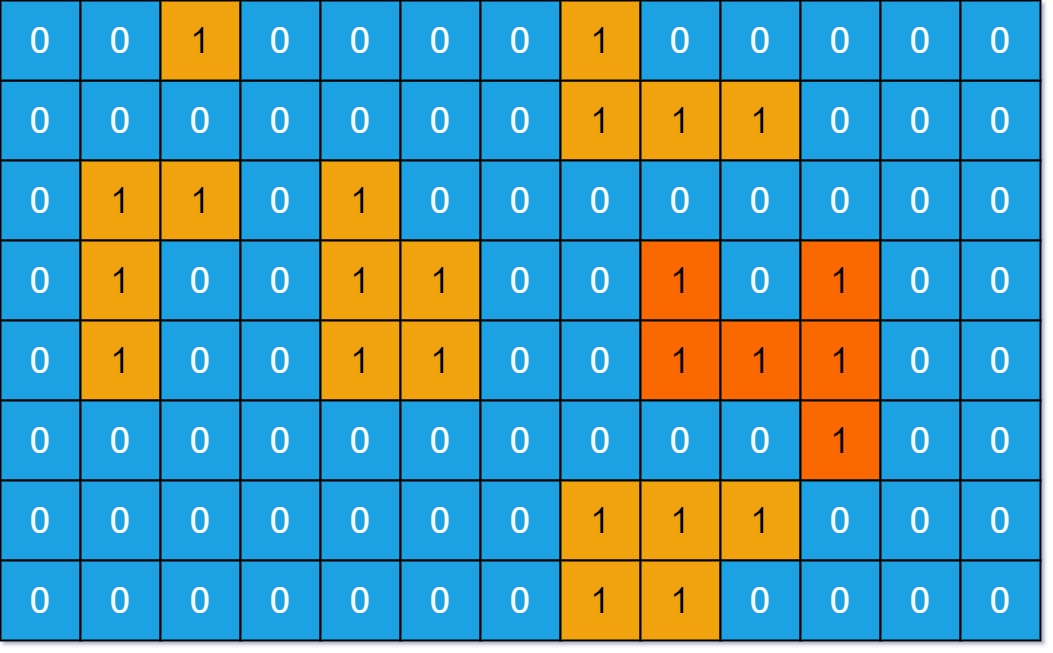
输入:grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
输出:6
解释:答案不应该是 11 ,因为岛屿只能包含水平或垂直这四个方向上的 1 。
示例 2:
输入:grid = [[0,0,0,0,0,0,0,0]]
输出:0
思路:
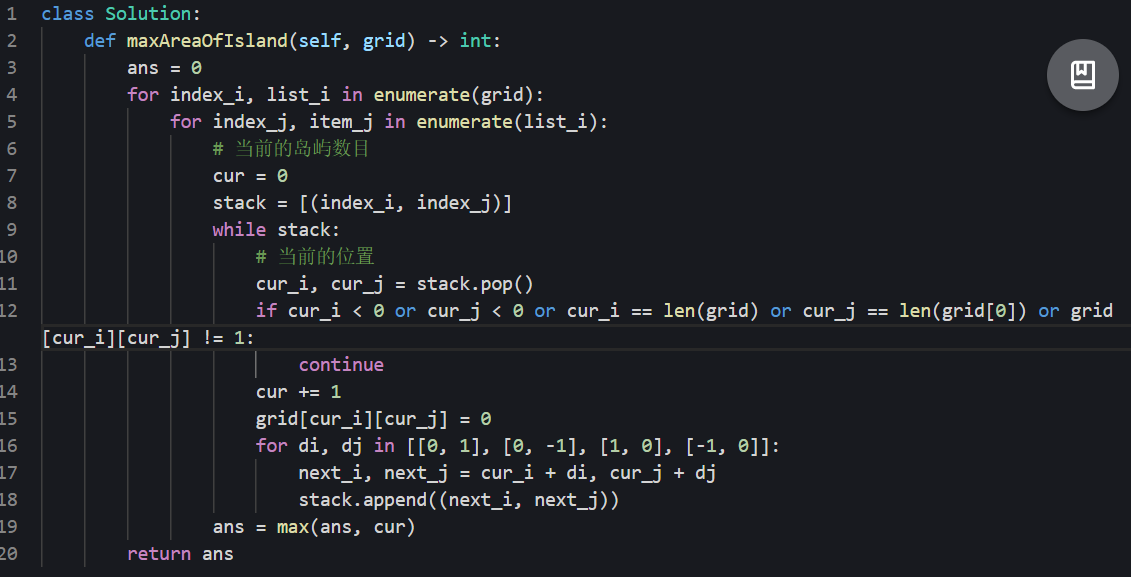
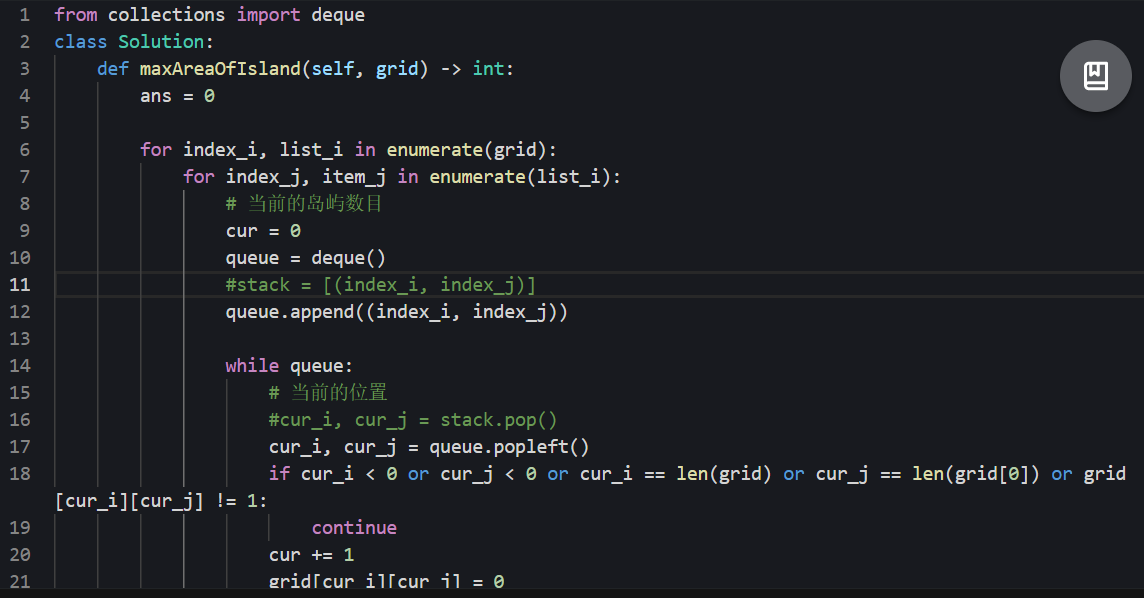
- 使用递归的方法,每次到达一块土地,如果当前位置没有超过边界,就朝四个方向探索
- 每次经过一次土地,就把他的值设置为0,避免被其他的四方向探索所访问

代码:

200. 岛屿数量
难度中等1476
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 1:
输入:grid = [
["1","1","1","1","0"],
["1","1","0","1","0"],
["1","1","0","0","0"],
["0","0","0","0","0"]
]
输出:1
示例 2:
输入:grid = [
["1","1","0","0","0"],
["1","1","0","0","0"],
["0","0","1","0","0"],
["0","0","0","1","1"]
]
输出:3
思路:
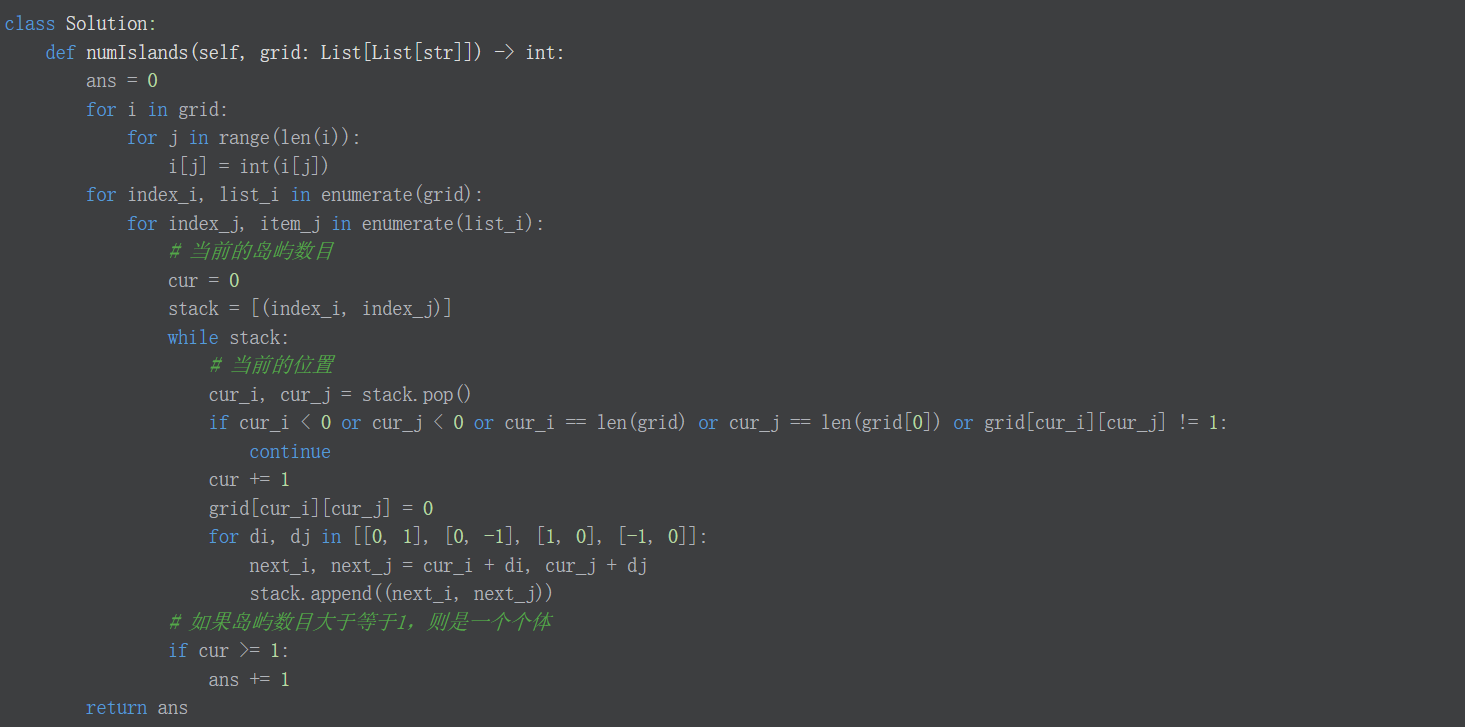
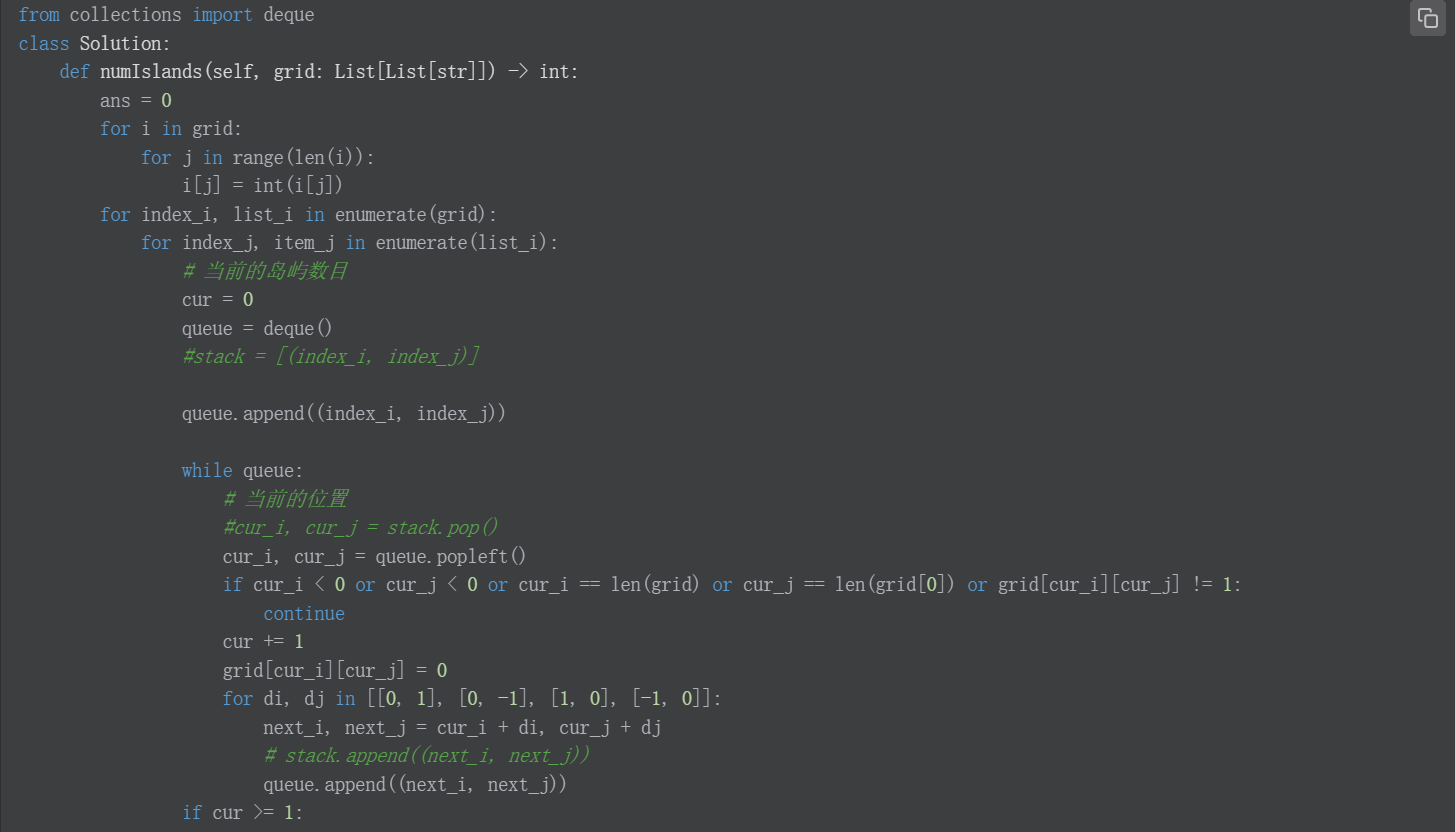
和上一题基本一致,只需要把str变为int,然后判断岛屿面积>=1
代码:

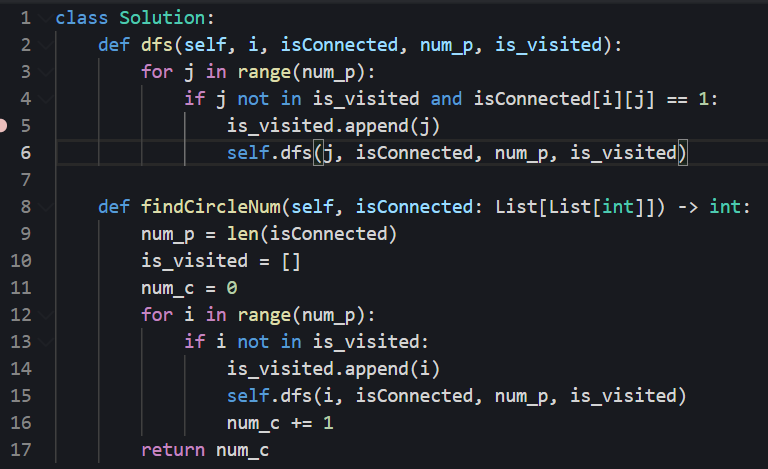
547. 省份数量
有 n 个城市,其中一些彼此相连,另一些没有相连。如果城市 a 与城市 b 直接相连,且城市 b 与城市 c 直接相连,那么城市 a 与城市 c 间接相连。
省份 是一组直接或间接相连的城市,组内不含其他没有相连的城市。
给你一个 n x n 的矩阵 isConnected ,其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连,而 isConnected[i][j] = 0 表示二者不直接相连。
返回矩阵中 省份 的数量。
示例 1:
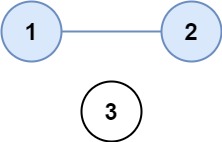
输入:isConnected = [[1,1,0],[1,1,0],[0,0,1]]
输出:2
示例 2:

输入:isConnected = [[1,0,0],[0,1,0],[0,0,1]]
输出:3
思路:
-
深度优先搜索
- 遍历所有城市,对于每个城市,如果该城市尚未被访问过,则从该城市开始深度优先搜索,通过矩阵 isConnected 得到与该城市直接相连的城市有哪些,这些城市和该城市属于同一个连通分量,然后对这些城市继续深度优先搜索,直到同一个连通分量的所有城市都被访问到,即可得到一个省份。遍历完全部城市以后,即可得到连通分量的总数,即省份的总数。
代码: