Binary Search Exercise 1

二分查找中使用的术语：

目标 Target —— 你要查找的值索引 Index —— 你要查找的当前位置左、右指示符 Left，Right —— 我们用来维持查找空间的指标中间指示符 Mid —— 我们用来应用条件来确定我们应该向左查找还是向右查找的索引

时间：O(log n) —— 算法时间

因为二分查找是通过对查找空间中间的值应用一个条件来操作的，并因此将查找空间折半，在更糟糕的情况下，我们将不得不进行 O(log n) 次比较，其中 n 是集合中元素的数目。

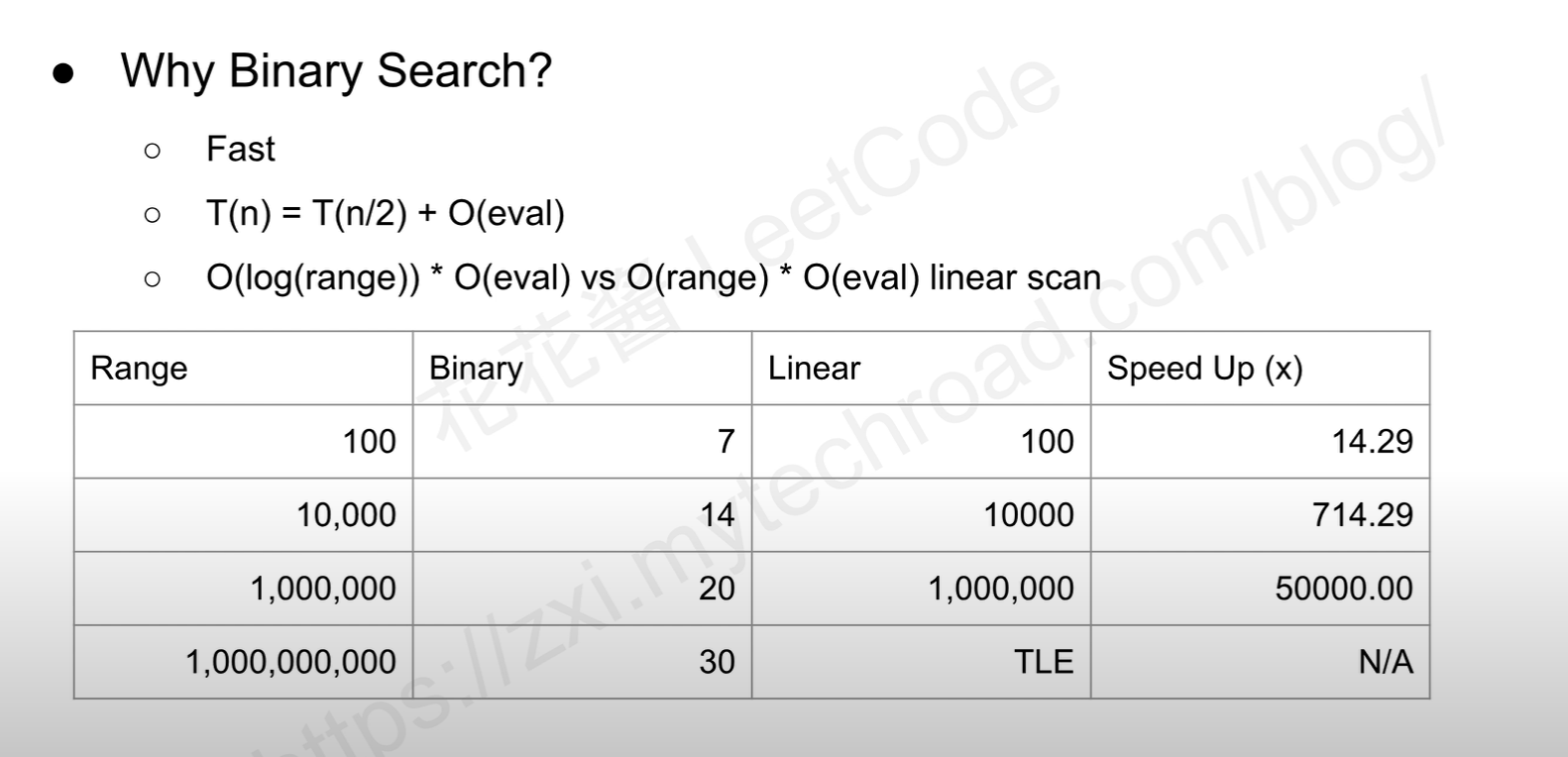
为什么是 log n？

二分查找是通过将现有数组一分为二来执行的。因此，每次调用子例程(或完成一次迭代)时，其大小都会减少到现有部分的一半。首先 N 变成 N/2，然后又变成 N/4，然后继续下去，直到找到元素或尺寸变为 1。迭代的最大次数是 log N (base 2) 。

感觉最难的就在于while的left是小于等于还是小于right

注意每次都是划分为三个区域

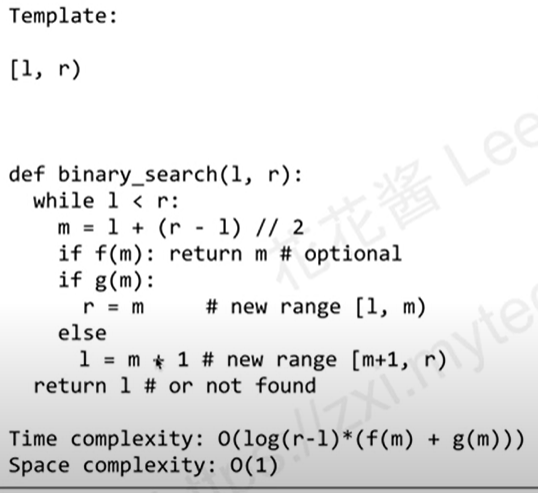
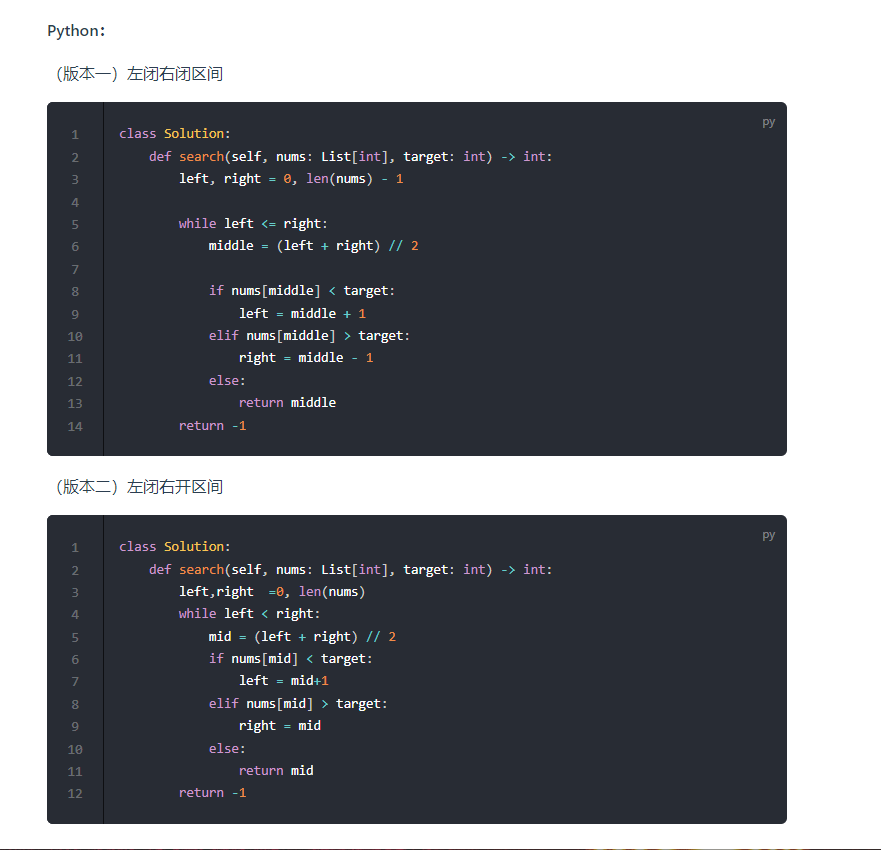
二分查找模板

使用右闭区间很容易会出现问题

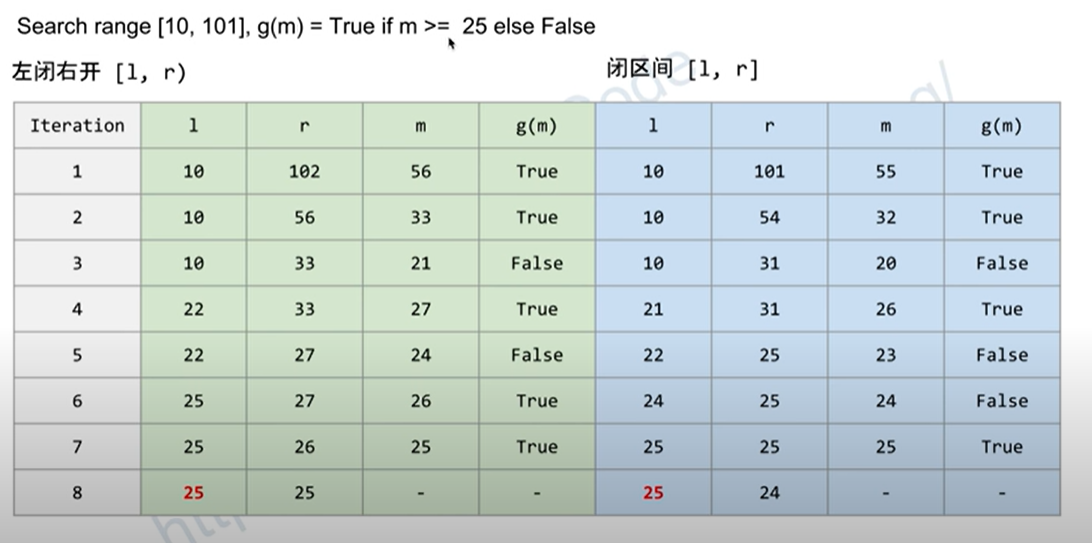
再来看一下278题

左闭右开就一个问题，可能会溢出，需要后处理

上题不会，但是对于开根号会有可能溢出，但是Python不存在这个问题
注意这面是找的upper bound
==所以用下面这个！==

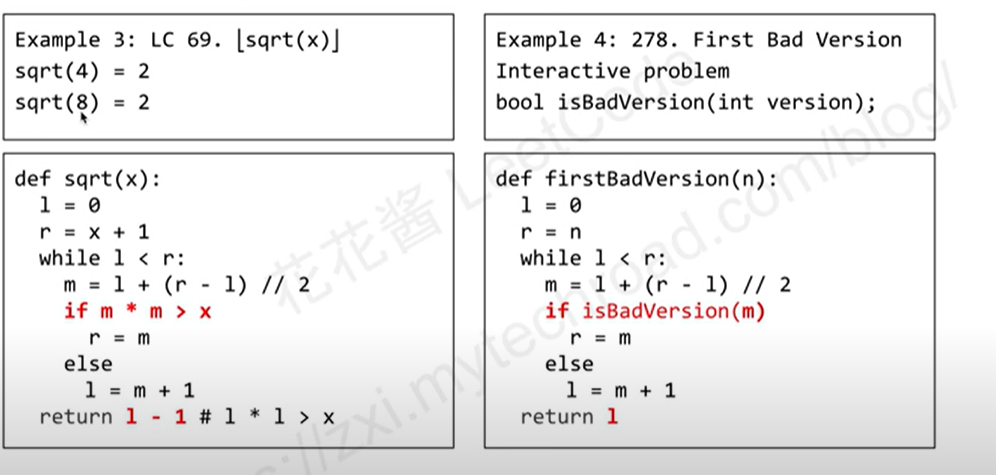
看个例子，找特定数字的index

看个例子，左边的是大于等于，右边是严格大于
大于等于用于lower
大于用于upper

看下leetcode 69这道题，注意这里找到的l是第一个平方严格大于x的，注意right这面是x+1
对于278，就不用改模板

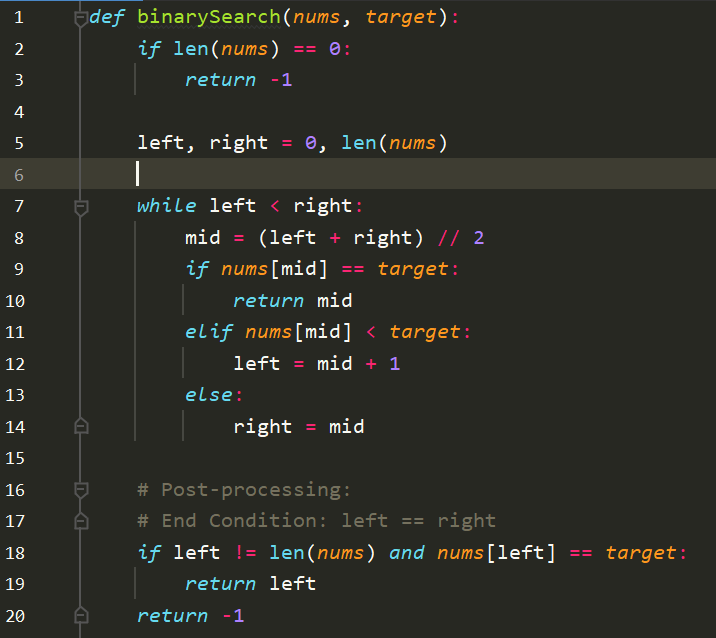
搜索左侧边界

「搜索区间」是 [left, right) 左闭右开，所以当 nums[mid] 被检测之后，下一步的搜索区间应该去掉 mid 分割成两个区间，即 [left, mid) 或 [mid + 1, right)。

二分搜索题目分类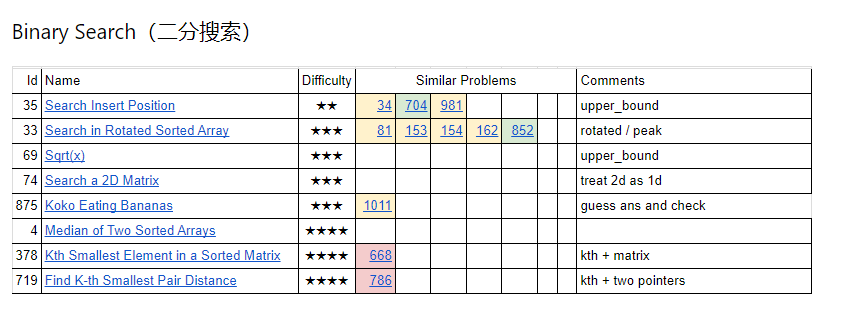

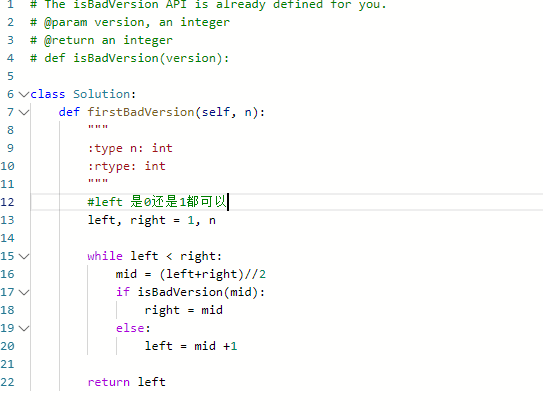
278. 第一个错误的版本

难度简单650

你是产品经理，目前正在带领一个团队开发新的产品。不幸的是，你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的，所以错误的版本之后的所有版本都是错的。

假设你有 n 个版本 [1, 2, ..., n]，你想找出导致之后所有版本出错的第一个错误的版本。

你可以通过调用 bool isBadVersion(version) 接口来判断版本号 version 是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数。

示例 1：

输入：n = 5, bad = 4
输出：4
解释：
调用 isBadVersion(3) -> false 
调用 isBadVersion(5) -> true 
调用 isBadVersion(4) -> true
所以，4 是第一个错误的版本。

示例 2：

输入：n = 1, bad = 1
输出：1

思路：

注意这里的是从1开始的，所以定义left和right时要注意
我们要找到的是版本是正好左边是好的，右边是坏的
每次我们都找到其中间的版本，检查其是否为正确版本。
- 如果为正确版本，那么第一个错误的版本必然位于该版本的右侧；
- 否则第一个错误的版本必然位于该版本及该版本的左侧，我们缩紧右边界。
注意我们希望API调用的越少越好，所以不可以在知道right是badversion后在对right+1和right-1检测，这样的风险太高

代码：

34. 在排序数组中查找元素的第一个和最后一个位置

难度中等1602

给定一个按照升序排列的整数数组 nums，和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

进阶：

你可以设计并实现时间复杂度为 O(log n) 的算法解决此问题吗？

示例 1：

输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]

示例 2：

输入：nums = [5,7,7,8,8,10], target = 6
输出：[-1,-1]

示例 3：

输入：nums = [], target = 0
输出：[-1,-1]

提示：

0 <= nums.length <= 105
-109 <= nums[i] <= 109
nums 是一个非递减数组
-109 <= target <= 109

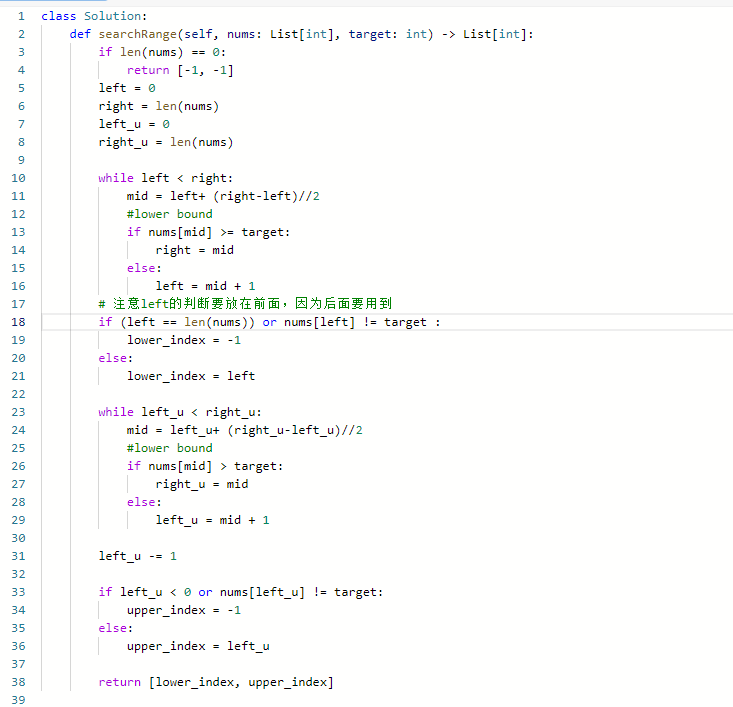
思路：

还是用模板
难点在于要注意left索引判断放在or前面
还有上界的left_u要减一
还有就是下界是防止left >= len(nums),这是不存在的索引
上界是防止left<0也是不存在的

代码：

35. 搜索插入位置

难度简单1478

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为 O(log n) 的算法。

示例 1:

输入: nums = [1,3,5,6], target = 5
输出: 2

示例 2:

输入: nums = [1,3,5,6], target = 2
输出: 1

示例 3:

输入: nums = [1,3,5,6], target = 7
输出: 4

提示:

1 <= nums.length <= 104
-104 <= nums[i] <= 104
nums 为 无重复元素 的升序排列数组
-104 <= target <= 104

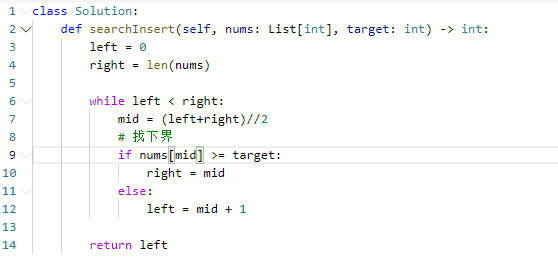
思路：

代码：

704. 二分查找

难度简单759

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

示例 1:

输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

示例 2:

输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1

提示：

你可以假设 nums 中的所有元素是不重复的。
n 将在 [1, 10000]之间。
nums 的每个元素都将在 [-9999, 9999]之间。

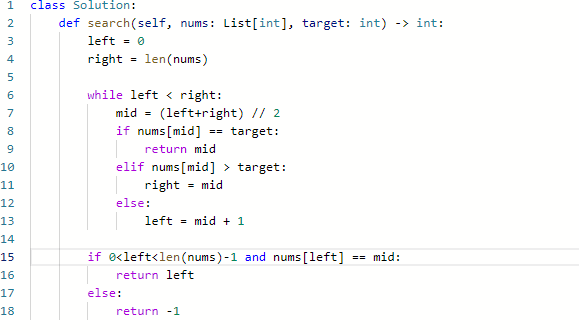
思路

注意不论在elif处用大于等于还是大于，都会通过，因为前者是返回下界，后者是返回上界，在这里都是同一个位置，因为不存在重复
注意left在返回前都要检测一下

代码：

981. 基于时间的键值存储

难度中等164

设计一个基于时间的键值数据结构，该结构可以在不同时间戳存储对应同一个键的多个值，并针对特定时间戳检索键对应的值。

实现 TimeMap 类：

TimeMap() 初始化数据结构对象
void set(String key, String value, int timestamp) 存储键 key、值 value，以及给定的时间戳 timestamp。
```
String get(String key, int timestamp)
```
- 返回先前调用 set(key, value, timestamp_prev) 所存储的值，其中 timestamp_prev <= timestamp 。
- 如果有多个这样的值，则返回对应最大的 timestamp_prev 的那个值。
- 如果没有值，则返回空字符串（""）。

示例：

输入：
["TimeMap", "set", "get", "get", "set", "get", "get"]
[[], ["foo", "bar", 1], ["foo", 1], ["foo", 3], ["foo", "bar2", 4], ["foo", 4], ["foo", 5]]
输出：
[null, null, "bar", "bar", null, "bar2", "bar2"]

解释：
TimeMap timeMap = new TimeMap();
timeMap.set("foo", "bar", 1);  // 存储键 "foo" 和值 "bar" ，时间戳 timestamp = 1   
timeMap.get("foo", 1);         // 返回 "bar"
timeMap.get("foo", 3);         // 返回 "bar", 因为在时间戳 3 和时间戳 2 处没有对应 "foo" 的值，所以唯一的值位于时间戳 1 处（即 "bar"） 。
timeMap.set("foo", "bar2", 4); // 存储键 "foo" 和值 "bar2" ，时间戳 timestamp = 4  
timeMap.get("foo", 4);         // 返回 "bar2"
timeMap.get("foo", 5);         // 返回 "bar2"

提示：

1 <= key.length, value.length <= 100
key 和 value 由小写英文字母和数字组成
1 <= timestamp <= 107
set 操作中的时间戳 timestamp 都是严格递增的
最多调用 set 和 get 操作 2 * 105 次

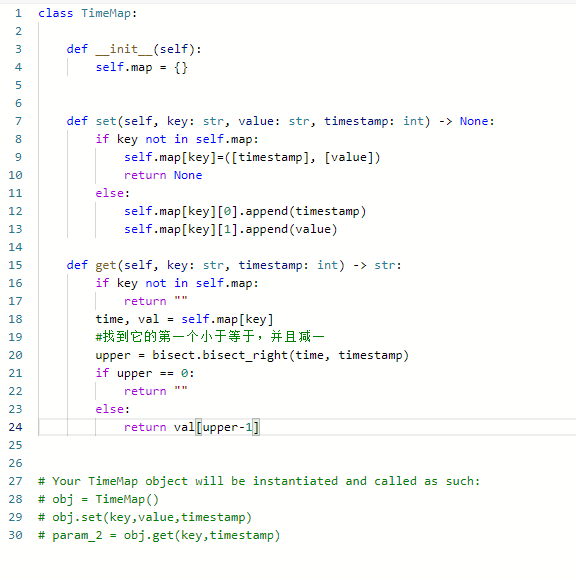
思路：

维护一个有序字典，并且使用二分查找来找到最大的timestamp
但是要用到Python3自带的二分查找库函数：bisect.bisect_right(), 来找到第一个小于等于

代码：

33. 搜索旋转排序数组

难度中等1986

整数数组 nums 按升序排列，数组中的值 互不相同 。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了旋转，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。

给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

示例 1：

输入：nums = [4,5,6,7,0,1,2], target = 0
输出：4

示例 2：

输入：nums = [4,5,6,7,0,1,2], target = 3
输出：-1

示例 3：

输入：nums = [1], target = 0
输出：-1

思路：

代码：

81. 搜索旋转排序数组 II

难度中等573

已知存在一个按非降序排列的整数数组 nums ，数组中的值不必互不相同。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了旋转，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,4,4,5,6,6,7] 在下标 5 处经旋转后可能变为 [4,5,6,6,7,0,1,2,4,4] 。

给你 旋转后 的数组 nums 和一个整数 target ，请你编写一个函数来判断给定的目标值是否存在于数组中。如果 nums 中存在这个目标值 target ，则返回 true ，否则返回 false 。

你必须尽可能减少整个操作步骤。

示例 1：

输入：nums = [2,5,6,0,0,1,2], target = 0
输出：true

示例 2：

输入：nums = [2,5,6,0,0,1,2], target = 3
输出：false

思路：

代码：

153. 寻找旋转排序数组中的最小值

难度中等716

已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次旋转后，得到输入数组。例如，原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到：

若旋转 4 次，则可以得到 [4,5,6,7,0,1,2]
若旋转 7 次，则可以得到 [0,1,2,4,5,6,7]

注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。

给你一个元素值 互不相同 的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

输入：nums = [3,4,5,1,2]
输出：1
解释：原数组为 [1,2,3,4,5] ，旋转 3 次得到输入数组。

示例 2：

输入：nums = [4,5,6,7,0,1,2]
输出：0
解释：原数组为 [0,1,2,4,5,6,7] ，旋转 4 次得到输入数组。

示例 3：

输入：nums = [11,13,15,17]
输出：11
解释：原数组为 [11,13,15,17] ，旋转 4 次得到输入数组。

154. 寻找旋转排序数组中的最小值 II & 剑指 Offer 11. 旋转数组的最小数字

难度简单593

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。

给你一个可能存在重复元素值的数组 numbers ，它原来是一个升序排列的数组，并按上述情形进行了一次旋转。请返回旋转数组的最小元素。例如，数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一次旋转，该数组的最小值为 1。

注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。

示例 1：

输入：numbers = [3,4,5,1,2]
输出：1

示例 2：

输入：numbers = [2,2,2,0,1]
输出：0

162. 寻找峰值

难度中等775

峰值元素是指其值严格大于左右相邻值的元素。

给你一个整数数组 nums，找到峰值元素并返回其索引。数组可能包含多个峰值，在这种情况下，返回 任何一个峰值 所在位置即可。

你可以假设 nums[-1] = nums[n] = -∞ 。

你必须实现时间复杂度为 O(log n) 的算法来解决此问题。

示例 1：

输入：nums = [1,2,3,1]
输出：2
解释：3 是峰值元素，你的函数应该返回其索引 2。

示例 2：

输入：nums = [1,2,1,3,5,6,4]
输出：1 或 5 
解释：你的函数可以返回索引 1，其峰值元素为 2；
     或者返回索引 5， 其峰值元素为 6。

思路：

看到O(lgn)，首先想到的就是二分查找

但是先想想其他的

看到说峰值严格比其他大，其实就遍历一遍数组，找到最大的，然后保存index就好了。但是这样的复杂度为O(n)
提到峰值，就想让 nums[i] 跟 nums[i-1], nums[i+1] 都比较一下，但其实只需要找出是单调递增还是单调递减就行了。
如果递增，nums[mid] < nums[mid+1], 那么峰值一定在mid的右边，left = mid+1
- 让我困惑的是为什么left要加一，但是不加一，确实有问题，left和right最后缩不到一起

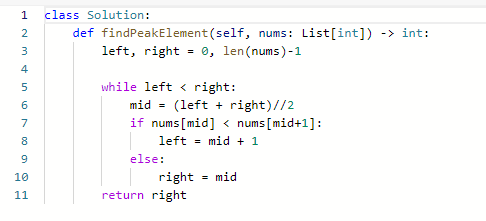
代码：

在常规的二分模板中，直接使用 right = len(nums), right 遍历过程中是取不到 len(nums)这个值的
而在这里再减去 1，主要是为了避免 nums[mid+1] 数组越界，而且又不妨碍最终的答案落在 len(nums) - 1 上

852. 山脉数组的峰顶索引

难度简单246

符合下列属性的数组 arr 称为 山脉数组 ：

arr.length >= 3
存在
```
i
```
（
```
0 < i < arr.length - 1
```
）使得：
- arr[0] < arr[1] < ... arr[i-1] < arr[i]
- arr[i] > arr[i+1] > ... > arr[arr.length - 1]

给你由整数组成的山脉数组 arr ，返回任何满足 arr[0] < arr[1] < ... arr[i - 1] < arr[i] > arr[i + 1] > ... > arr[arr.length - 1] 的下标 i 。

示例 1：

输入：arr = [0,1,0]
输出：1

示例 2：

输入：arr = [0,2,1,0]
输出：1

示例 3：

输入：arr = [0,10,5,2]
输出：1

示例 4：

输入：arr = [3,4,5,1]
输出：2

示例 5：

输入：arr = [24,69,100,99,79,78,67,36,26,19]
输出：2

提示：

3 <= arr.length <= 104
0 <= arr[i] <= 106
题目数据保证 arr 是一个山脉数组

进阶：很容易想到时间复杂度 O(n) 的解决方案，你可以设计一个 O(log(n)) 的解决方案吗？

69. Sqrt(x)

难度简单835

给你一个非负整数 x ，计算并返回 x 的 算术平方根 。

由于返回类型是整数，结果只保留 整数部分 ，小数部分将被 舍去。

注意：不允许使用任何内置指数函数和算符，例如 pow(x, 0.5) 或者 x ** 0.5 。

示例 1：

输入：x = 4
输出：2

示例 2：

输入：x = 8
输出：2
解释：8 的算术平方根是 2.82842..., 由于返回类型是整数，小数部分将被舍去。

分析：

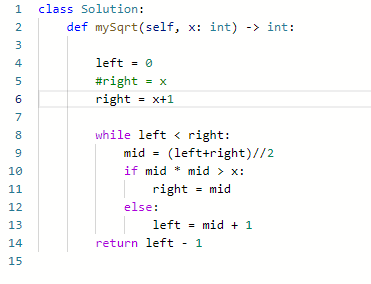
设定上下区间进行二分查找，复杂度为O(lgn)
注意一般left用作下限，right因为本来就是开区间，所以应该是上限加一
回想之前的数组，right是用len(nums)，这是取不到的，而left用的是0
所以这里right用x+1，因为x可以被取到

代码：

74. 搜索二维矩阵

难度中等617

编写一个高效的算法来判断 m x n 矩阵中，是否存在一个目标值。该矩阵具有如下特性：

每行中的整数从左到右按升序排列。
每行的第一个整数大于前一行的最后一个整数。

示例 1：

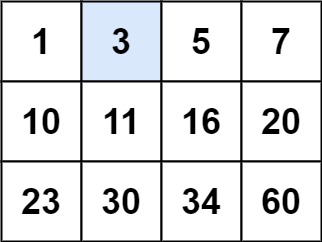
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出：true

示例 2：

输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
输出：false

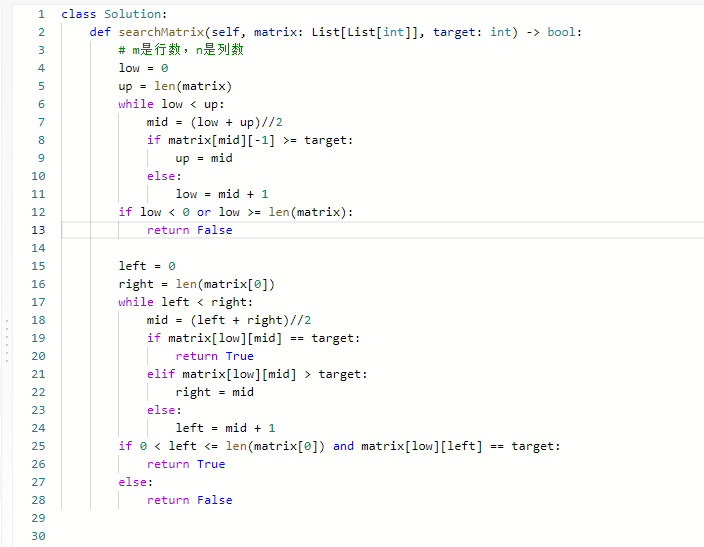
思路：

代码：

875. 爱吃香蕉的珂珂 & 剑指 Offer II 073. 狒狒吃香蕉

难度中等277

珂珂喜欢吃香蕉。这里有 N 堆香蕉，第 i 堆中有 piles[i] 根香蕉。警卫已经离开了，将在 H 小时后回来。

珂珂可以决定她吃香蕉的速度 K （单位：根/小时）。每个小时，她将会选择一堆香蕉，从中吃掉 K 根。如果这堆香蕉少于 K 根，她将吃掉这堆的所有香蕉，然后这一小时内不会再吃更多的香蕉。

珂珂喜欢慢慢吃，但仍然想在警卫回来前吃掉所有的香蕉。

返回她可以在 H 小时内吃掉所有香蕉的最小速度 K（K 为整数）。

示例 1：

输入: piles = [3,6,7,11], H = 8 输出: 4 示例 2：

输入: piles = [30,11,23,4,20], H = 5 输出: 30 示例 3：

输入: piles = [30,11,23,4,20], H = 6 输出: 23

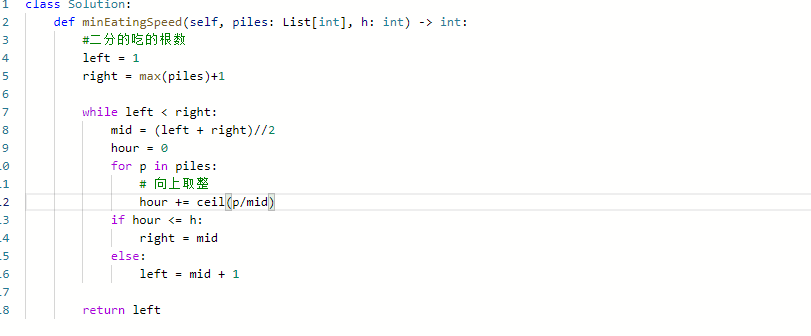
思路：

可以看如下的伪代码：
下界left应可以找到的最小值，珂珂最少吃一根1，上界是开区间，应该找到最大值+1。注意不是piles的长度，而是取值
- 其中容易出错的点在于
难点在于向上取整的写法
- Python 提供的向上取整使用ceil()
- 或者是result = （分母+分子-1) / 分子
这道题是最左二分，也就是求下界

代码：

时间复杂度：O(NlogW)，其中 NN* 是香蕉堆的数量，WW 最大的香蕉堆的大小。
空间复杂度：O(1)

1011. 在 D 天内送达包裹的能力

难度中等453

传送带上的包裹必须在 days 天内从一个港口运送到另一个港口。

传送带上的第 i 个包裹的重量为 weights[i]。每一天，我们都会按给出重量（weights）的顺序往传送带上装载包裹。我们装载的重量不会超过船的最大运载重量。

返回能在 days 天内将传送带上的所有包裹送达的船的最低运载能力。

示例 1：

输入：weights = [1,2,3,4,5,6,7,8,9,10], days = 5
输出：15
解释：
船舶最低载重 15 就能够在 5 天内送达所有包裹，如下所示：
第 1 天：1, 2, 3, 4, 5
第 2 天：6, 7
第 3 天：8
第 4 天：9
第 5 天：10

请注意，货物必须按照给定的顺序装运，因此使用载重能力为 14 的船舶并将包装分成 (2, 3, 4, 5), (1, 6, 7), (8), (9), (10) 是不允许的。 

示例 2：

输入：weights = [3,2,2,4,1,4], days = 3
输出：6
解释：
船舶最低载重 6 就能够在 3 天内送达所有包裹，如下所示：
第 1 天：3, 2
第 2 天：2, 4
第 3 天：1, 4

示例 3：

输入：weights = [1,2,3,1,1], days = 4
输出：3
解释：
第 1 天：1
第 2 天：2
第 3 天：3
第 4 天：1, 1

提示：

1 <= days <= weights.length <= 5 * 104
1 <= weights[i] <= 500

思路：

代码：

Binary Search Exercise 1