Array/String Exercise 1
27. 移除元素
难度简单1149
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
说明:
为什么返回数值是整数,但输出的答案是数组呢?
请注意,输入数组是以「引用」方式传递的,这意味着在函数里修改输入数组对于调用者是可见的。
你可以想象内部操作如下:
// nums 是以“引用”方式传递的。也就是说,不对实参作任何拷贝
int len = removeElement(nums, val);
// 在函数里修改输入数组对于调用者是可见的。
// 根据你的函数返回的长度, 它会打印出数组中 该长度范围内 的所有元素。
for (int i = 0; i < len; i++) {
print(nums[i]);
}
示例 1:
输入:nums = [3,2,2,3], val = 3
输出:2, nums = [2,2]
解释:函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。例如,函数返回的新长度为 2 ,而 nums = [2,2,3,3] 或 nums = [2,2,0,0],也会被视作正确答案。
示例 2:
输入:nums = [0,1,2,2,3,0,4,2], val = 2
输出:5, nums = [0,1,4,0,3]
解释:函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。注意这五个元素可为任意顺序。你不需要考虑数组中超出新长度后面的元素。
思路:
-
暴力法:
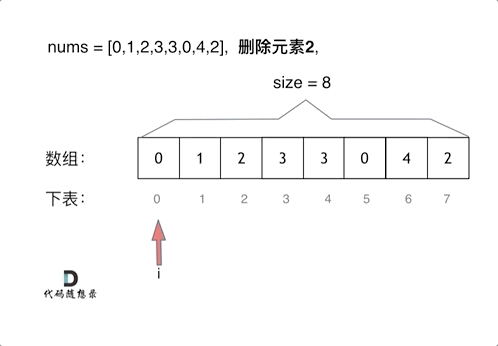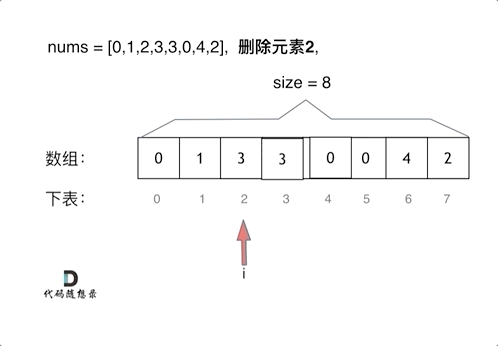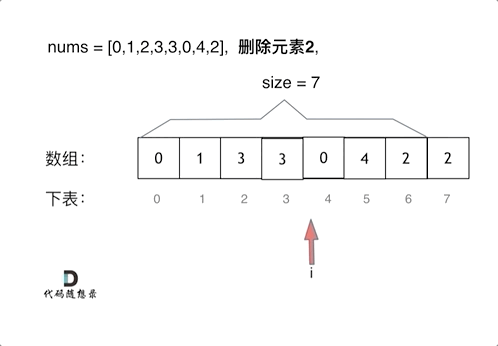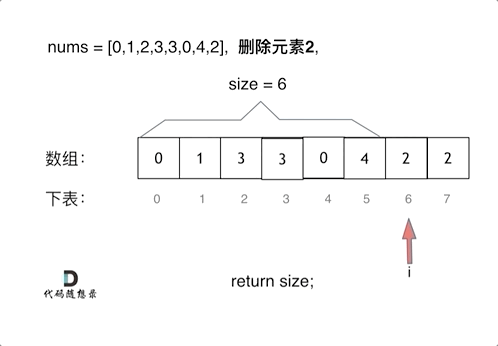
-
双指针法:
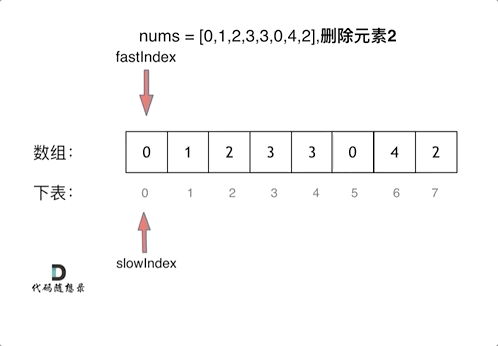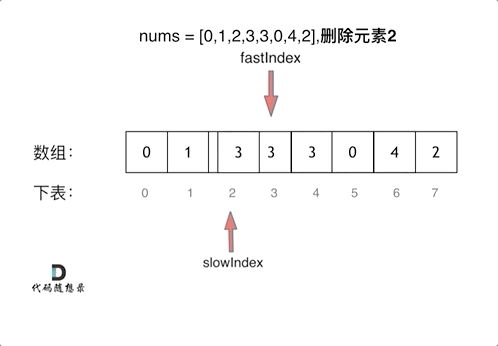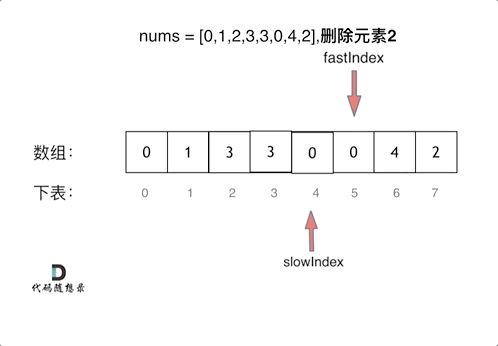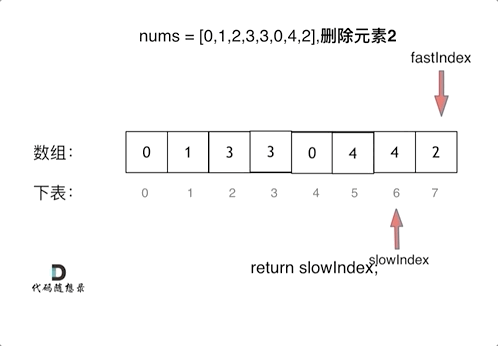
-
fast指针每次while循环都会向前。而slow指针只会在fast指针指的不是要删除元素时才会向前
-
每次slow指针要动时,会和fast指针交换信息
-
注意最后要return slow来确定长度
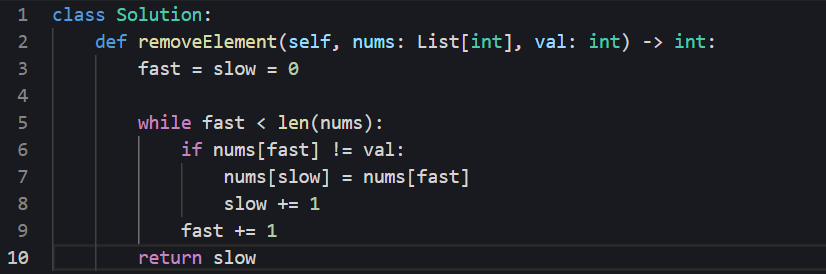
代码:
977. 有序数组的平方
难度简单405
给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。
示例 1:
输入:nums = [-4,-1,0,3,10]
输出:[0,1,9,16,100]
解释:平方后,数组变为 [16,1,0,9,100]
排序后,数组变为 [0,1,9,16,100]
示例 2:
输入:nums = [-7,-3,2,3,11]
输出:[4,9,9,49,121]
思路:
- 如果使用暴力法,也就是全部平方后再排序,会是O(n\log n)的复杂度
- 这道题使用双指针法:
- 首先一个指针指向尾部,一个指向头部
- 显然最大的平方数要么就是在尾部,要么就是头部
- 那么两者比较,谁大,谁就放在result最后面

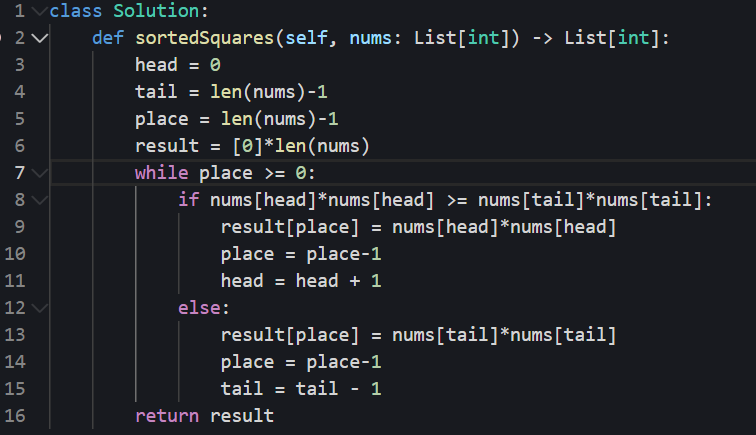
代码:
209. 长度最小的子数组
难度中等894
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
示例 1:
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。
示例 2:
输入:target = 4, nums = [1,4,4]
输出:1
示例 3:
输入:target = 11, nums = [1,1,1,1,1,1,1,1]
输出:0
思路:
- 如果使用暴力法,相当于是两个for循环是O(n^2)
- 这里使用滑动窗口,类似于双指针。存储一个变量result来保存当前见过最小的长度
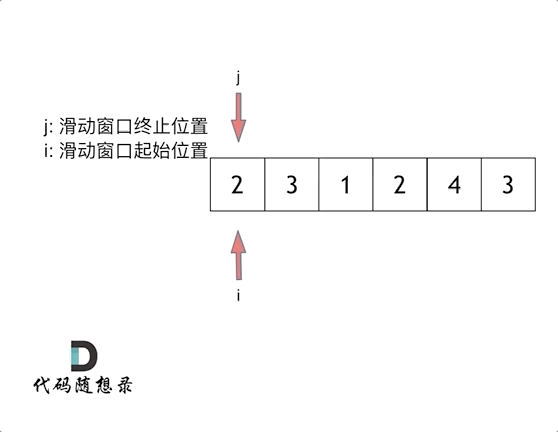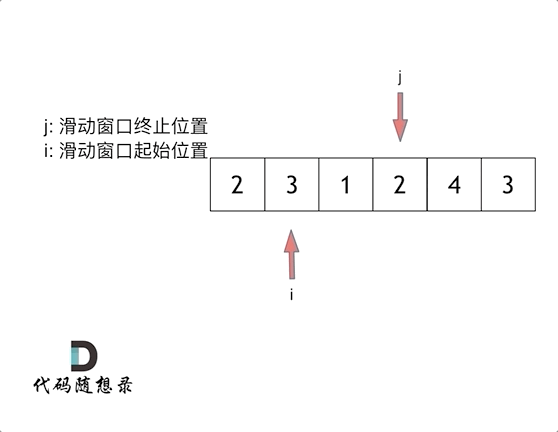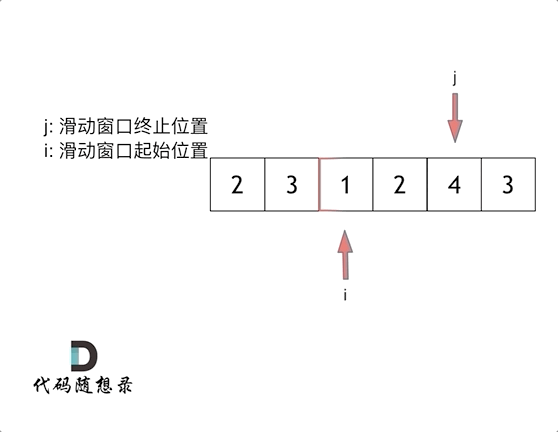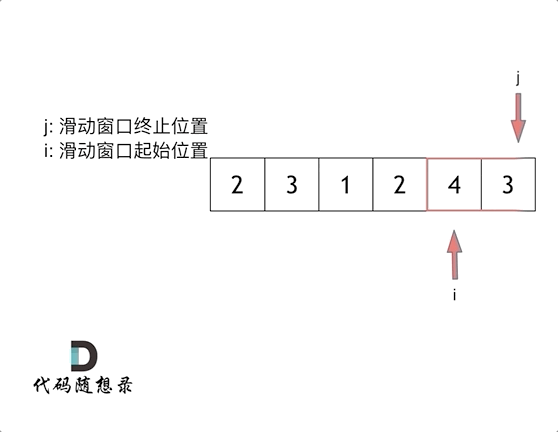
- 首先初始化result为一个不可能存在的较大的结果,比如
len(nums)+1,最后检验result如果仍然是这个值,返回0,说明没有这样的字串
代码:

59. 螺旋矩阵 II
难度中等574
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
示例 1:
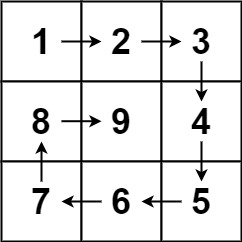
输入:n = 3
输出:[[1,2,3],[8,9,4],[7,6,5]]
示例 2:
输入:n = 1
输出:[[1]]
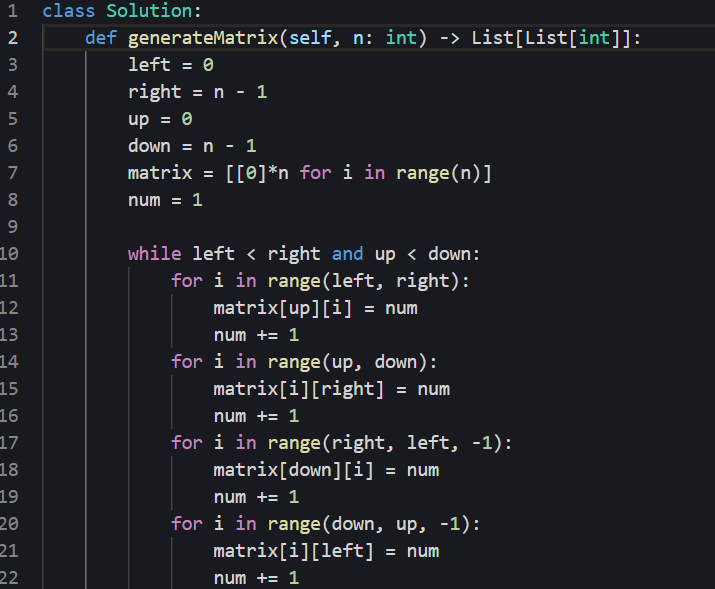
思路:
- 遵循左闭右开的原则,在拐弯处让给新的一条边
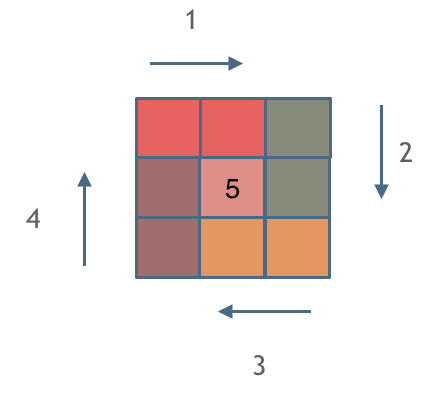
- 首先是初始化矩阵,比如输入3,我们初始化是[[0,0,0],[0,0,0],[0,0,0]]。也就是[[0]*n for i in range(n)]
- 其次是确定边界
- 初始:left = 0; right = n - 1; up = 0; down = n - 1
- 其中从下往上和从右往左这种倒序的表达方式:

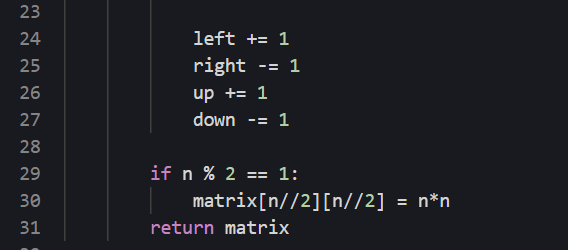
- 迭代一轮后,left += 1; right -= 1 up += 1 down -= 1
- 然后是循环的终止条件,是up <down 并且 left < right,而不是相等,因为偶的情况将直接超过那个位置
- 最后是确定特殊情况,如果n是偶数,就是一直转圈,不用到中心。如果n是奇数,需要判断
- 首先是奇数的判断方法:
n%2
- 首先是奇数的判断方法:
代码: