Dynamic Programming Exercise 1

动态规划和贪心的区别？
- 贪心没有状态推导，而是从局部直接选最优的
- 动态规划中每一个状态一定是由上一个状态推导出来的
对于动态规划问题五步曲
1. 确定dp数组（dp table）以及下标的含义
2. 确定递推公式
3. dp数组如何初始化
4. 确定遍历顺序
5. 举例推导dp数组

1. 基础题目

509. 斐波那契数

难度简单405收藏分享切换为英文接收动态反馈

斐波那契数 （通常用 F(n) 表示）形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：

F(0) = 0，F(1) = 1
F(n) = F(n - 1) + F(n - 2)，其中 n > 1

给定 n ，请计算 F(n) 。

示例 1：

输入：n = 2
输出：1
解释：F(2) = F(1) + F(0) = 1 + 0 = 1

示例 2：

输入：n = 3
输出：2
解释：F(3) = F(2) + F(1) = 1 + 1 = 2

示例 3：

输入：n = 4
输出：3
解释：F(4) = F(3) + F(2) = 2 + 1 = 3

思路：

第一步，确定dp数组的意义：dp[i]代表第i个斐波那契数的值
第二步，确定递推公式：dp[i] = dp[i-1]+dp[i-2]
第三步，dp数组初始化：dp[0] = 0, dp[1] = 1
第四步，确定遍历顺序：从前往后
第五步，举例子来验证

代码：

70. 爬楼梯

难度简单2221收藏分享切换为英文接收动态反馈

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

示例 1：

输入：n = 2
输出：2
解释：有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶

示例 2：

输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶

思路：

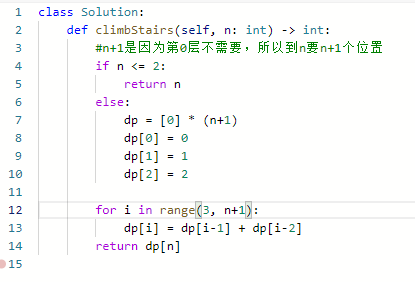
第一步，确定dp[i]的含义：i层楼有几种爬法
第二步，确定递推公式：dp[i] = dp[i-1] *1+dp[i-2] *1
- 到第i层，无非是在i-1层走了一步或者在i-2层走了两步
第三步确定初始化：dp[1] = 1, dp[2] = 2
第四步确定遍历顺序：从i-1和i-2推i，显然是从前往后
第五步：举例子

之后第四第五步可以不要了

代码：

时间和空间复杂度都是O(n), 有空间O(1)的方法

746. 使用最小花费爬楼梯

难度简单814收藏分享切换为英文接收动态反馈

给你一个整数数组 cost ，其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用，即可选择向上爬一个或者两个台阶。

你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。

请你计算并返回达到楼梯顶部的最低花费。

示例 1：

输入：cost = [10,15,20]
输出：15
解释：你将从下标为 1 的台阶开始。
- 支付 15 ，向上爬两个台阶，到达楼梯顶部。
总花费为 15 。

示例 2：

输入：cost = [1,100,1,1,1,100,1,1,100,1]
输出：6
解释：你将从下标为 0 的台阶开始。
- 支付 1 ，向上爬两个台阶，到达下标为 2 的台阶。
- 支付 1 ，向上爬两个台阶，到达下标为 4 的台阶。
- 支付 1 ，向上爬两个台阶，到达下标为 6 的台阶。
- 支付 1 ，向上爬一个台阶，到达下标为 7 的台阶。
- 支付 1 ，向上爬两个台阶，到达下标为 9 的台阶。
- 支付 1 ，向上爬一个台阶，到达楼梯顶部。
总花费为 6 。

思路：

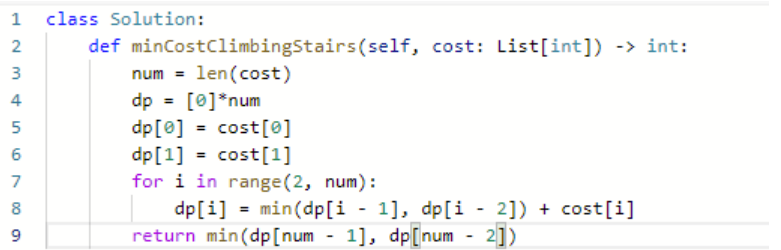
dp[i] 是第i层的最低花费
因为是一定要走到底，所以不用纠结dp是n还是n-1，只要用和cost的长度和下标一样就行
默认每一步都要收费，但如果是最后一步，就不收费
- 这是很重要的，就是决定了dp的递推公式是加c[i], 而最后return的是dp[i-1]和dp[i-2]中小的那个
递推关系是什么？第i层的最低花费是min（第i层的花费加上前i-1的最低花费，第i层的花费加上前i-2的最低花费）。
- dp[i] = min(dp[i-1], dp[i-2]) +c[i]
初始化：dp[0] = c[0], dp[1] = c[1]

代码：

62. 不同路径

难度中等1288收藏分享切换为英文接收动态反馈

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：

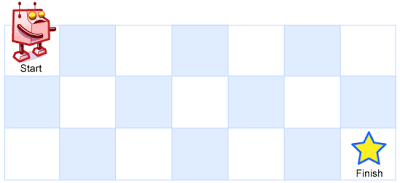
输入：m = 3, n = 7
输出：28

示例 2：

输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下

示例 3：

输入：m = 7, n = 3
输出：28

示例 4：

输入：m = 3, n = 3
输出：6

思路：

首先是dp[i,j]，到达i，j点有几种路径
dp[i] [j]=dp[i-1] [j]+dp[i] [j-1]: 只可能是从上面或者下面来的
~~dp[0, 0] = 1~~整个dp都初始化为1
这里的初始化方法要注意（二阶的初始化）：里面的for是行，这样每一行都是一个长为n的list
注意把每个点的值初始化为一，这样每走一步都能加一次
时间和空间复杂度都是O（m*n）

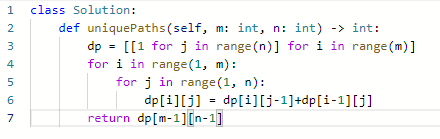
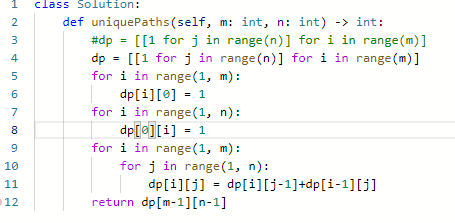
代码：

可以一开始都当1，思路清晰的话，应该是边缘是1

63. 不同路径 II

难度中等736收藏分享切换为英文接收动态反馈

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

示例 1：

输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出：2
解释：3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右

示例 2：

输入：obstacleGrid = [[0,1],[0,0]]
输出：1

思路：

相比上一道题，区别就是需要在遍历dp时，需要进行判断，只有没有障碍时，才能使用递推式
第一步，确定dp: dp[i] [j]代表从(0,0)到i，j的路线数目
第二步，确定递推式：加上障碍判断的dp[i] [j]=dp[i-1] [j]+dp[i] [j-1]，如果有障碍就保持原样，等迭代过掉这个点
第三步，初始化：不同于之前的全部为1，这里应该注意如果边缘的地方出现障碍，后面的位置都应该为0
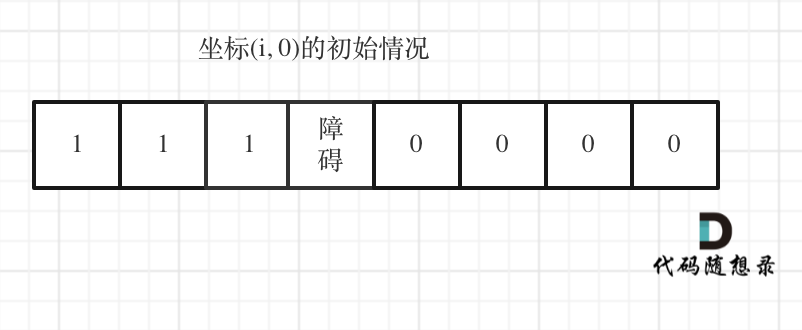
- 具体上要判断第一个（0，0）位置是不是障碍，是，直接返回0
- 然后遍历整个dp的两边，赋值1，因为只写地方只有一种到达的方式
- 其他的地方就是dp计算就好了
注意，这里给的没有长和宽，要自己提取，提取的方式是
- 行数：
- 列数：

代码：

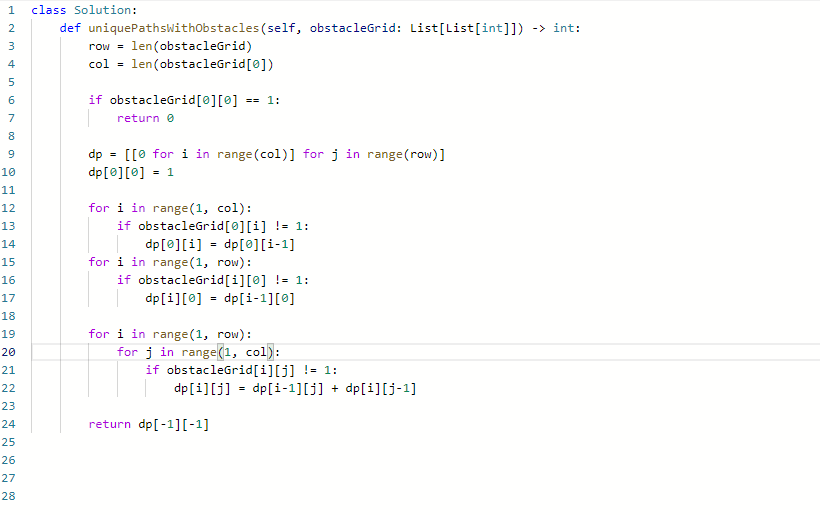
343. 整数拆分

难度中等722

给定一个正整数 n ，将其拆分为 k 个 正整数 的和（ k >= 2 ），并使这些整数的乘积最大化。

返回 你可以获得的最大乘积 。

示例 1:

输入: n = 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。

示例 2:

输入: n = 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36

思路：

dp[i]: 对于整数i的最大拆分
递推式：dp[i] = max{dp[i], dp[i-j] *j, (i-j) *j}
- 其中j是从1遍历到i-1
- dp[i-j] *j是对i-j进行计算最大拆分
- (i-j) *j是直接相乘
初始化：没必要考虑0和1，从dp[2] = 1开始

代码：

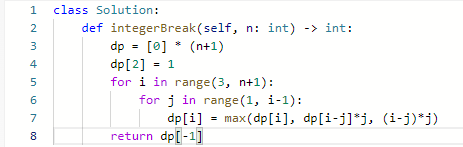
96. 不同的二叉搜索树

难度中等1579收藏分享切换为英文接收动态反馈

给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

示例 1：

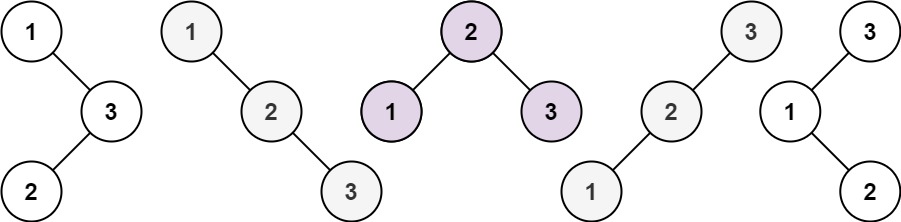
输入：n = 3
输出：5

示例 2：

输入：n = 1
输出：1

思路：

确定dp[i]的意义： 1到i为节点组成的二叉搜索树的个数为dp[i]
先举个例子：
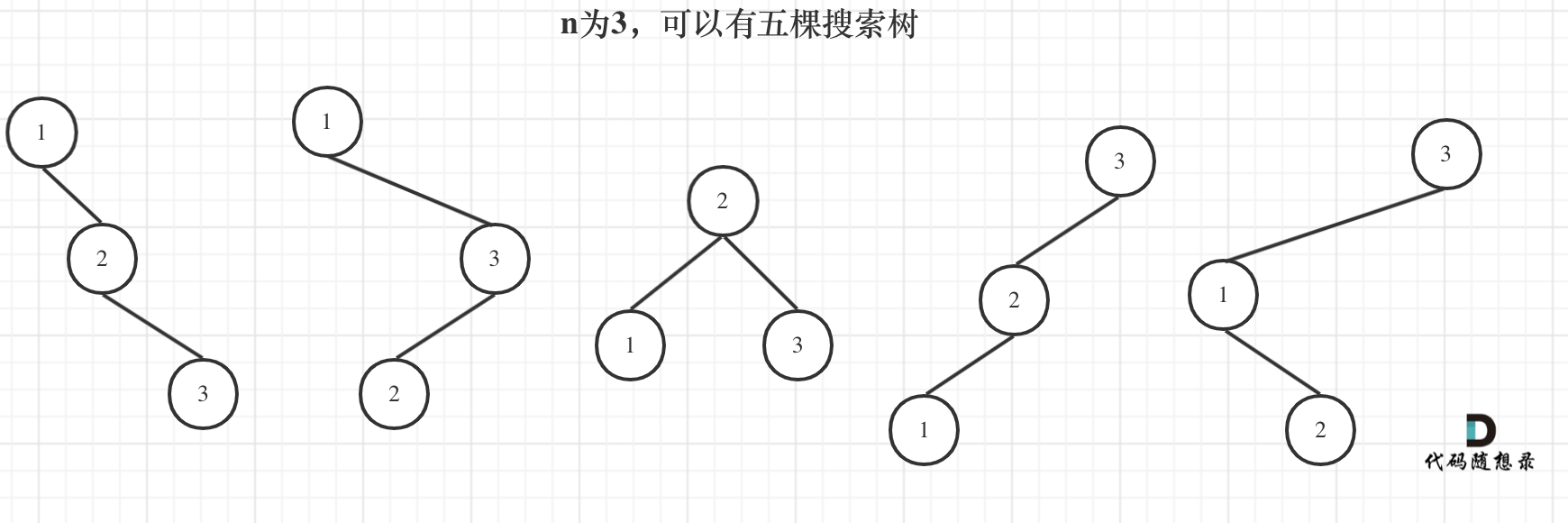
- 比如n = 3，我们考虑dp[3], 就是元素1为头结点搜索树的数量 + 元素2为头结点搜索树的数量 + 元素3为头结点搜索树的数量
- 元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量 = dp[2]*dp[0]
- 元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 * 左子树有1个元素的搜索树数量 = dp[1]*dp[1]
- 元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 * 左子树有2个元素的搜索树数量 = dp[0]*dp[2]
dp[i] = sum(dp[j]*dp[i-j-1]), 其中j从0到i-1
初始化：dp[0] = 1, dp[1] = 1

代码：

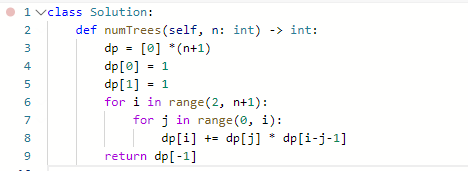
2. 背包问题

2.1 01背包

有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

举一个例子：

背包最大重量为4。

物品为：

	重量	价值
物品0	1	15
物品1	3	20
物品2	4	30

问背包能背的物品最大价值是多少？

dp数组的意义：即dp[i] [j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少
递推式：
- dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
- 放物品i：dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值；dp[i - 1][j - weight[i]] + value[i] 就是背包放物品i得到的最大价值
- 不放物品i：dp[i - 1][j](其实就是当物品i的重量大于背包j的重量时，物品i无法放进背包中，所以被背包内的价值依然和前面相同。)
初始化：
- 如果背包容量j为0，无论是选取哪些物品，背包价值总和一定为0：
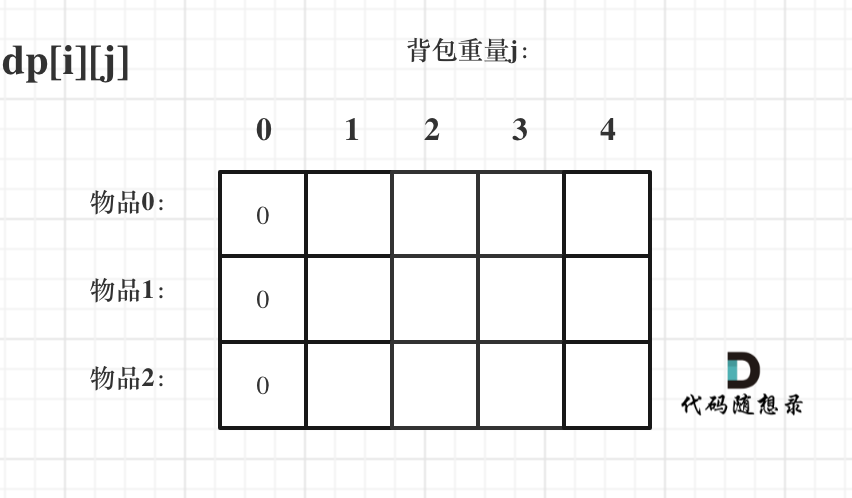
- i为0，存放编号0的物品的时候， j < weight[0]的时候，dp[0] [j] 应该是 0；j >= weight[0]时，dp[0] [j] 应该是value[0]，因为背包容量放足够放编号0物品
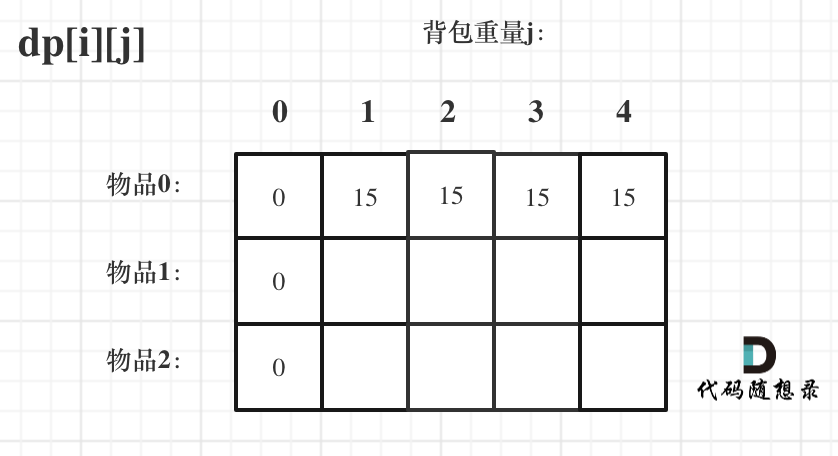
- 对于其他部分统一把dp数组统一初始为0，更方便一些
- 有两个遍历的维度：物品与背包重量；但是先遍历物品更好理解

如果使用一维滚动数组

状态压缩

dp[j]表示：容量为j的背包，所背的物品价值可以最大为dp[j]
dp[j]有两个选择，一个是取自己当前的dp[j] ，即不放物品i，一个是取dp[j - weight[i]] + value[i]，即放物品i。二者取最大
```
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
```
dp[j - weight[i]]表示容量为j - weight[i]的背包所背的最大价值。

dp[j - weight[i]] + value[i] 表示容量为j的背包，放入物品i了之后的价值
dp数组初始化的时候，都初始为0
遍历顺序与二维时不同，是倒序遍历，为了保证物品i只被放入一次！

416. Partition Equal Subset Sum

难度中等1232收藏分享切换为中文接收动态反馈

Given a non-empty array nums containing only positive integers, find if the array can be partitioned into two subsets such that the sum of elements in both subsets is equal.

Example 1:

Input: nums = [1,5,11,5]
Output: true
Explanation: The array can be partitioned as [1, 5, 5] and [11].

Example 2:

Input: nums = [1,2,3,5]
Output: false
Explanation: The array cannot be partitioned into equal sum subsets.

思路：

即一个商品如果可以重复多次放入是完全背包，而只能放入一次是01背包
本题要求集合里能否出现总和为 sum / 2 的子集
动态规划五部曲
- 确定dp数组以及下标的含义：dp[j]表示背包总容量是j，最大可以凑成j的子集总和为dp[j]
- 确定递推公式：01背包的递推公式为：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
  - dp[j - weight[i]]表示容量为j - weight[i]的背包所背的最大价值。
  - dp[j - weight[i]] + value[i] 表示容量为j的背包，放入物品i了之后的价值
  - 在这道题中，weight和value是等价的数值，所以是dp[j]=max(dp[j], dp[j-num[i]]+num[i])
- 如何初始化dp数组：都初始为0
- 确定遍历顺序：如果使用一维dp数组，物品遍历的for循环放在外层，遍历背包的for循环放在内层，且内层for循环倒序遍历！
  - for(int i = 0; i < nums.size(); i++) { for(int j = target; j >= nums[i]; j--) { // 每一个元素一定是不可重复放入，所以从大到小遍历 dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]); } }
- 举例推导dp数组：比如输入[1,5,11,5], 则target = (1+5+5+11)/2=11;我们希望看到dp[target] == target
对于i=0，对于容量为11~1的背包，最多存入1
对于i=1，也就是对于容量为11~6的背包，将最多存入1+5=6
对于i=2，也就是容量为11的背包，最多存入11，dp[11]会变成11
对于i=3，也就是容量为11-5的背包，将会在10哪里变一下

代码：

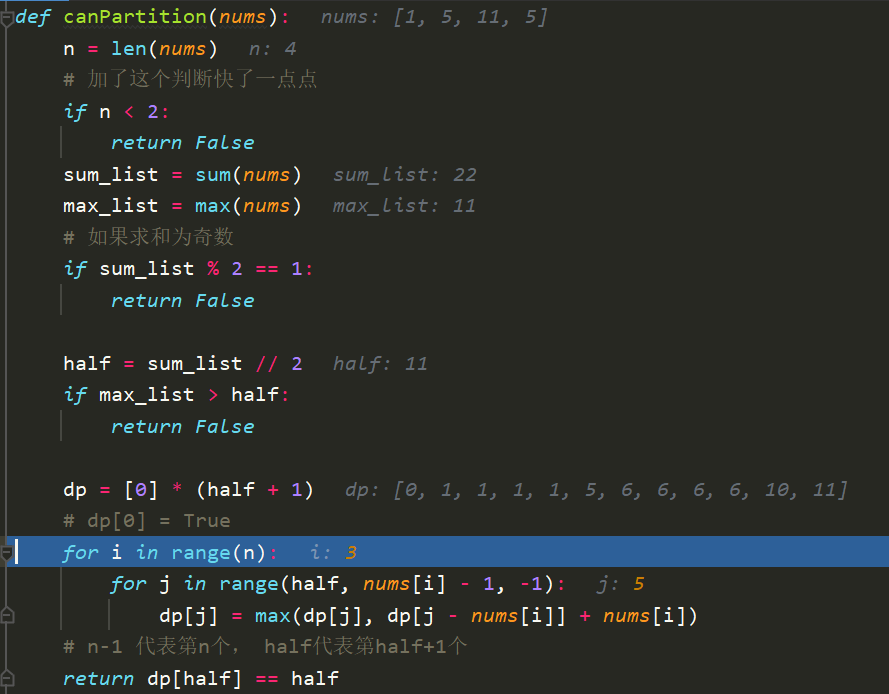
1049. Last Stone Weight II

难度中等419收藏分享切换为中文接收动态反馈

You are given an array of integers stones where stones[i] is the weight of the ith stone.

We are playing a game with the stones. On each turn, we choose any two stones and smash them together. Suppose the stones have weights x and y with x <= y. The result of this smash is:

If x == y, both stones are destroyed, and
If x != y, the stone of weight x is destroyed, and the stone of weight y has new weight y - x.

At the end of the game, there is at most one stone left.

Return the smallest possible weight of the left stone. If there are no stones left, return 0.

Example 1:

Input: stones = [2,7,4,1,8,1]
Output: 1
Explanation:
We can combine 2 and 4 to get 2, so the array converts to [2,7,1,8,1] then,
we can combine 7 and 8 to get 1, so the array converts to [2,1,1,1] then,
we can combine 2 and 1 to get 1, so the array converts to [1,1,1] then,
we can combine 1 and 1 to get 0, so the array converts to [1], then that's the optimal value.

Example 2:

Input: stones = [31,26,33,21,40]
Output: 5

思路：

将石头尽量分为重量相同的两堆，最优解就是这道题的答案
物品的重量等价于价值
动态规划五部曲
- 确定dp数组和下标含义：容量为j的背包，最多可以放dp[j]的物品
- 确定递推公式：dp[j]=max(dp[j],dp[j-stones[i]]+stones[i])
  - dp[j-stones[i]] 代表容量为j-stones[i]的背包，最大负重
- 初始化dp数组：全部初始化为0，长度是总重量的一半
- 确定遍历顺序：一维数组倒序遍历
- 举例：[2,4,1,1], half = 4
  
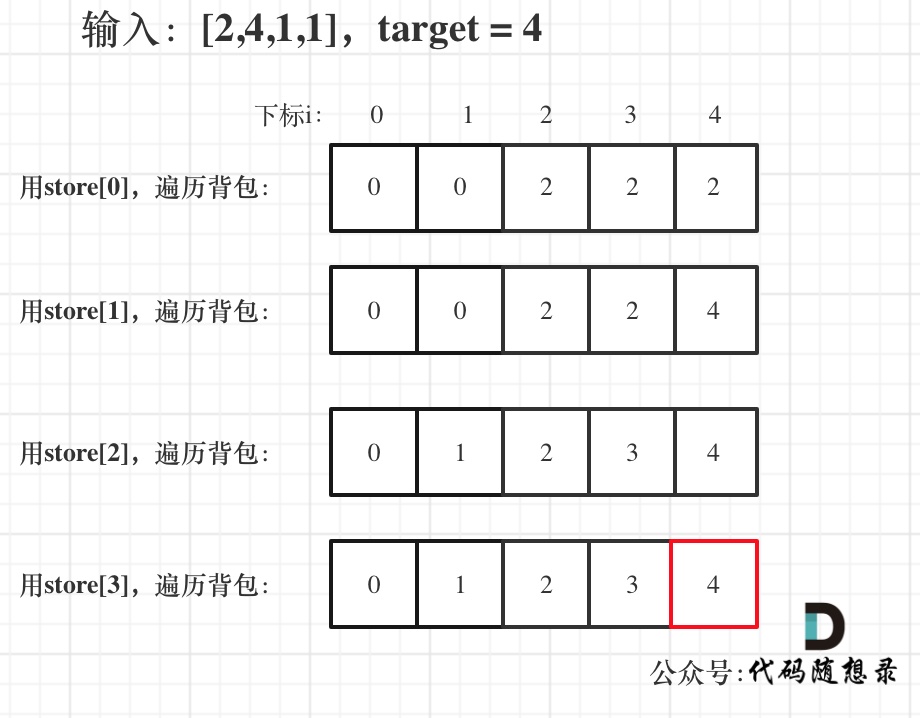
  最后dp[target]里是容量为target的背包所能背的最大重量。
  
  那么分成两堆石头，一堆石头的总重量是dp[target]，另一堆就是sum - dp[target]。
  
  相撞之后剩下的最小石头重量就是 (sum - dp[target]) - dp[target]
前一题是问是否能装满，这个是最多装多少，所以是sum-dp[half]-dp[half]

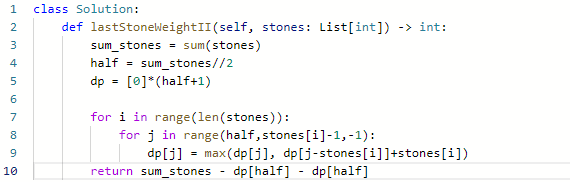
代码：

494. Target Sum

难度中等1143收藏分享切换为中文接收动态反馈

You are given an integer array nums and an integer target.

You want to build an expression out of nums by adding one of the symbols '+' and '-' before each integer in nums and then concatenate all the integers.

For example, if nums = [2, 1], you can add a '+' before 2 and a '-' before 1 and concatenate them to build the expression "+2-1".

Return the number of different expressions that you can build, which evaluates to target.

Example 1:

Input: nums = [1,1,1,1,1], target = 3
Output: 5
Explanation: There are 5 ways to assign symbols to make the sum of nums be target 3.
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3

Example 2:

Input: nums = [1], target = 1
Output: 1

思路：

假设有加号的部分叫x，有减号的部分叫sum-x

我们知道x-(sum-x)=target

所以x=(target+sum)/2

确定dp数组及其下标
- dp[j]表示装满容量为j的背包，有dp[j]种方法
- 不同于之前最多能装多少，这里是有方法的数目
确定递推公式
- 假如我们目标是5，我们有一个1，那么就有dp[4]种方法
- 同理，如果有2，就有dp[3]种方法…..
- 所以要求dp[j], 对于i从0~j进行遍历; dp[j] += dp[j-nums[i]]
初始化dp
- 对于dp[0]初始化为1，代表装满容量为0的背包的方法是1，什么都不放
- 对于其他的dp[j]初始化为0
确定遍历循序
- 外循环正序
- 内循环倒序
举例推导dp数组
- nums: [1, 1, 1, 1, 1], S: 3
- 我们可以知道加号的部分是（5+3）//2=4
- 也就是我们要凑出来一个+4和一个-1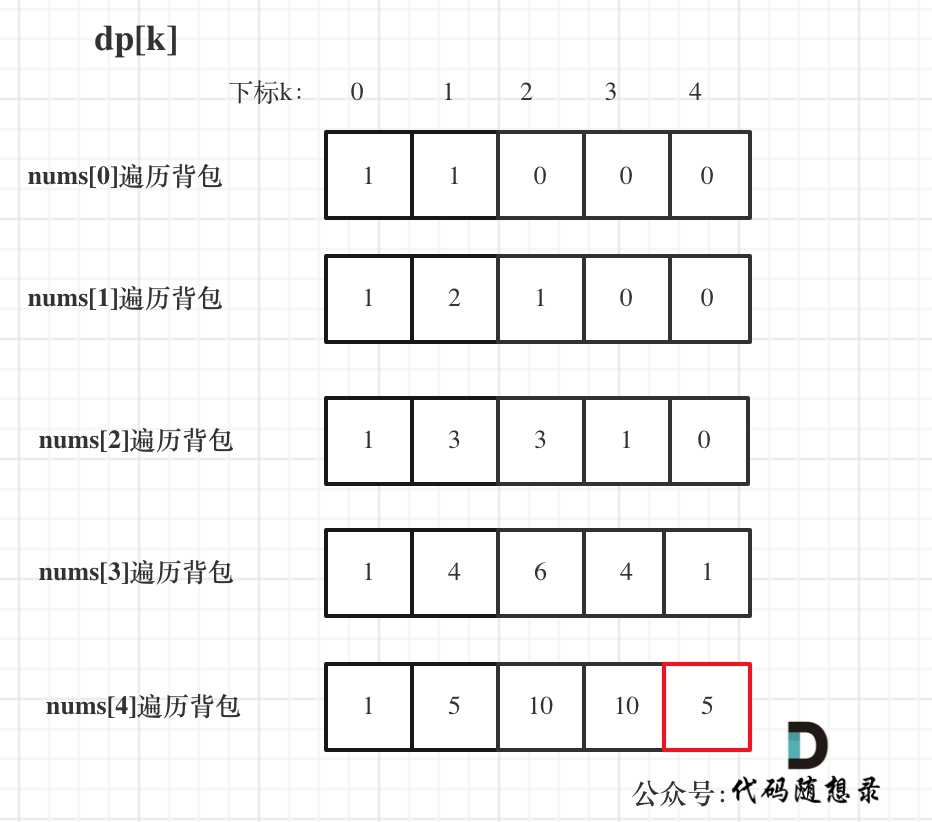

代码：

注意边界条件，如果target的绝对值太大，比整个list求和都大，不可以；或者全是加号的part不是整除，也是不行的。

这题的边界条件很多，要小心

注意内循环的上限是add_part,不是target

474. Ones and Zeroes

难度中等680收藏分享切换为中文接收动态反馈

You are given an array of binary strings strs and two integers m and n.

Return the size of the largest subset of strs such that there are at most m 0’s and n 1’s in the subset.

A set x is a subset of a set y if all elements of x are also elements of y.

Example 1:

Input: strs = ["10","0001","111001","1","0"], m = 5, n = 3
Output: 4
Explanation: The largest subset with at most 5 0's and 3 1's is {"10", "0001", "1", "0"}, so the answer is 4.
Other valid but smaller subsets include {"0001", "1"} and {"10", "1", "0"}.
{"111001"} is an invalid subset because it contains 4 1's, greater than the maximum of 3.

Example 2:

Input: strs = ["10","0","1"], m = 1, n = 1
Output: 2
Explanation: The largest subset is {"0", "1"}, so the answer is 2.

思路：

本题中strs 数组里的元素就是物品，每个物品都是一个！

而m 和 n相当于是一个背包，两个维度的背包,所以这回是dp[i] [j]

所以这是一个两个维度的01背包
确定dp数组和下标的意义
- dp[i] [j]代表最多有i个0和j个1的这个子集的长度
递推式
- dp[i] [j]纳入一个str，而这个str种有n_0个0和n_1个1，那么dp[i] [j] = dp[i - str_0] [j - str_1]+1
- 所以dp[i] [j] = max(dp[i] [j], dp[i - str_0] [j - str_1]+1)
确定遍历顺序：
- 之前一直说内循环要倒序，其实更明确的说是在遍历背包容量时需要从前往后遍历
举例

代码：

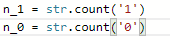
从str种计算字符的个数：

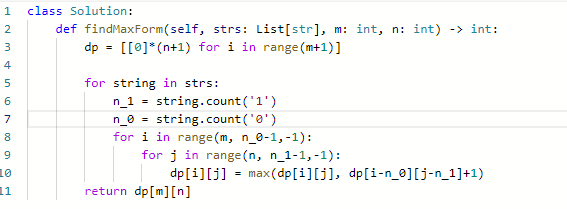
2.2 完全背包

有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品都有无限个（也就是可以放入背包多次），求解将哪些物品装入背包里物品价值总和最大。

完全背包和01背包问题唯一不同的地方就是，每种物品有无限件。

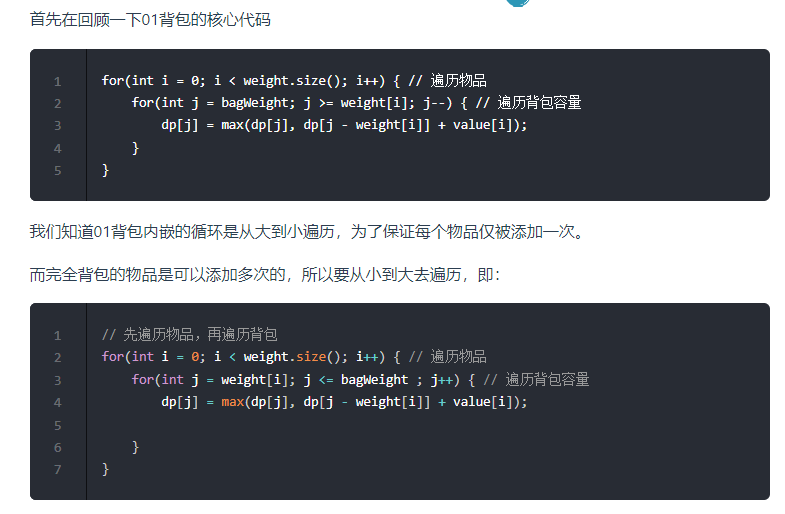
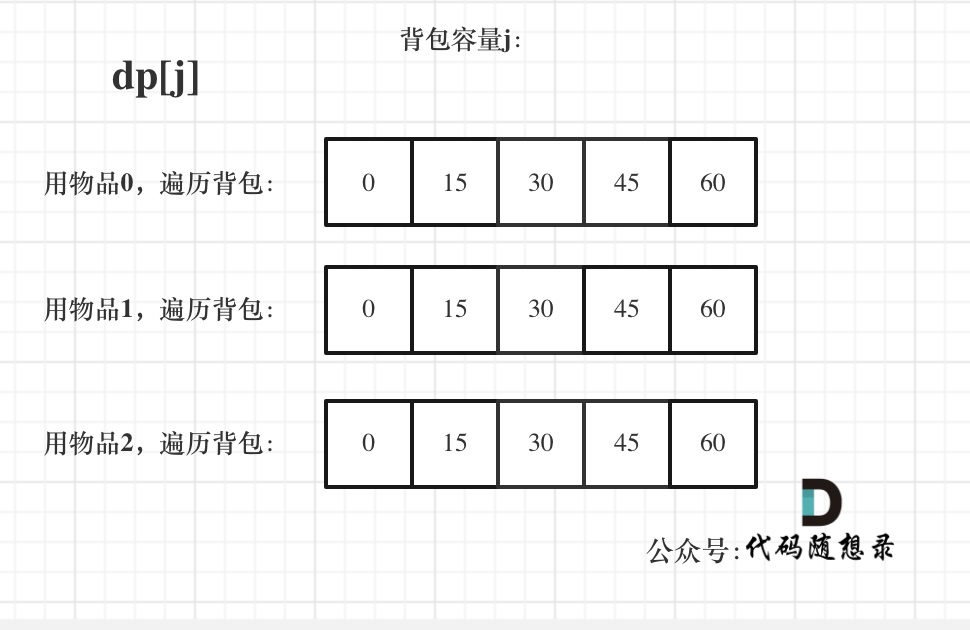
动态规划-完全背包

其实还有一个很重要的问题，为什么遍历物品在外层循环，遍历背包容量在内层循环？

01背包中二维dp数组的两个for遍历的先后循序是可以颠倒
01背包中一维dp数组的两个for循环先后循序一定是先遍历物品，再遍历背包容量。
完全背包种一维dp数组也可以颠倒顺序

在完全背包中，对于一维dp数组来说，其实两个for循环嵌套顺序同样无所谓！

518. Coin Change 2

难度中等767

You are given an integer array coins representing coins of different denominations and an integer amount representing a total amount of money.

Return the number of combinations that make up that amount. If that amount of money cannot be made up by any combination of the coins, return 0.

You may assume that you have an infinite number of each kind of coin.

The answer is guaranteed to fit into a signed 32-bit integer.

Example 1:

Input: amount = 5, coins = [1,2,5]
Output: 4
Explanation: there are four ways to make up the amount:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1

Example 2:

Input: amount = 3, coins = [2]
Output: 0
Explanation: the amount of 3 cannot be made up just with coins of 2.

Example 3:

Input: amount = 10, coins = [10]
Output: 1

思路：

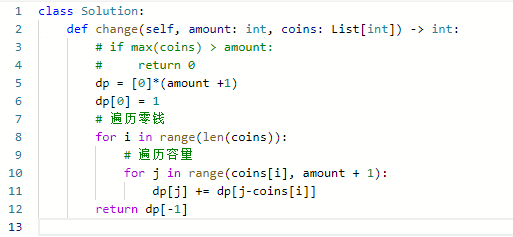
本题和纯完全背包不一样，纯完全背包是能否凑成总金额，而本题是要求凑成总金额的个数！
确定dp数组和下标的含义：dp[j]代表总金额j有dp[j]种组合
确定递推公式：与494 Target Sum类似的，对于i从0~j进行遍历; dp[j] += dp[j-nums[i]]
- 可以理解为对于j这个上限，不断拿各个nums[i]来试着减去，然后看后面的部分有多少种方法。nums[i]一定被使用
初始化dp数组：dp[0] = 1,其余为0
确定遍历的顺序
- 不同于常见的完全背包不考虑两个for循环的顺序
举例子
- 输入: amount = 5, coins = [1, 2, 5] ，dp状态图如下：

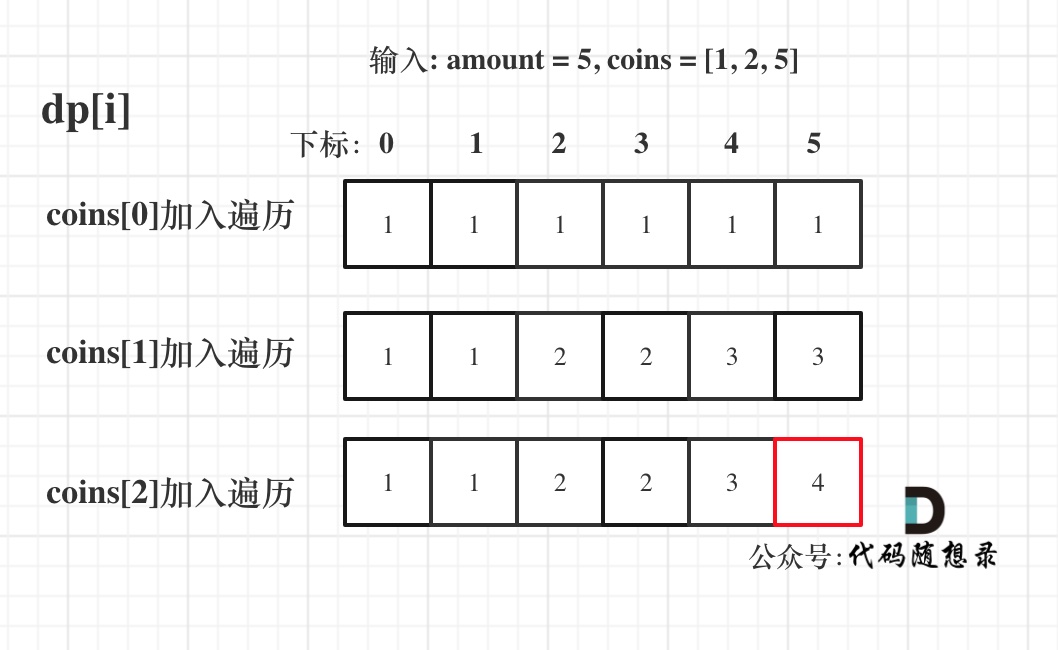
代码：

在求装满背包有几种方案的时候，认清遍历顺序是非常关键的。

如果求组合数就是外层for循环遍历物品，内层for遍历背包。

如果求排列数就是外层for遍历背包，内层for循环遍历物品。

初始化的长度取决于j，j代表容量，dp[j]代表方案的个数

注意dp[0] = 1! 这样递归才能开始

注意内循环是从coins[i]开始的，内部的起始值很关键

不能用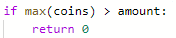这个来判断，因为这样的方式不是0。实际就是不找了，这也是一种方式

377. Combination Sum IV

难度中等600

Given an array of distinct integers nums and a target integer target, return the number of possible combinations that add up to target.

The test cases are generated so that the answer can fit in a 32-bit integer.

Example 1:

Input: nums = [1,2,3], target = 4
Output: 7
Explanation:
The possible combination ways are:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
Note that different sequences are counted as different combinations.

Example 2:

Input: nums = [9], target = 3
Output: 0

Follow up: What if negative numbers are allowed in the given array? How does it change the problem? What limitation we need to add to the question to allow negative numbers?

思路：

这道题就是就排列顺序的，不想上一题是单纯的组合
确定dp数组和下标：dp[j], target为j时有dp[j]种排列
确定递推公式：dp[j] += dp[j-nums[i]]
- 看了这么多题，可以得出一个经验性的结论：对于装满背包的问题，常用的递推式为dp[j] += dp[j-nums[i]]
确定初始化dp[0] = 1,其余为0
确定遍历顺序
- 如果求组合数就是外层for循环遍历物品，内层for遍历背包。
  
  如果求排列数就是外层for遍历背包，内层for循环遍历物品。
举例

代码：

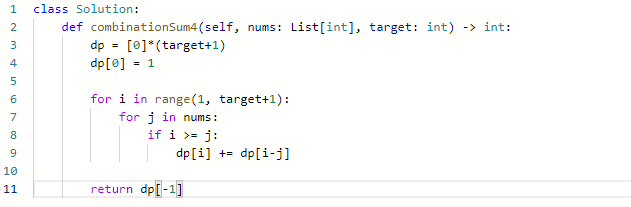
没太搞明白

70. Climbing Stairs

难度简单2325

You are climbing a staircase. It takes n steps to reach the top.

Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?

Example 1:

Input: n = 2
Output: 2
Explanation: There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 steps

Example 2:

Input: n = 3
Output: 3
Explanation: There are three ways to climb to the top.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step

思路：

可以理解为完全背包
确定dp和下标
- dp[n]代表到n层楼梯有几种走法
确定递推式
- dp[n] += dp[n-j]
- j只可能是1或者2，也就是走一步还是走两步
确定dp数组初始化
- dp[0] = 1
确定遍历顺序
- 和上一题一样，这是推导排列顺序的问题
- 所以外层遍历容量，内层是遍历物品
- 如果是组合就是外层遍历物品，内存遍历容量
- 为什么？之后要会给别人解释。
举例

代码：

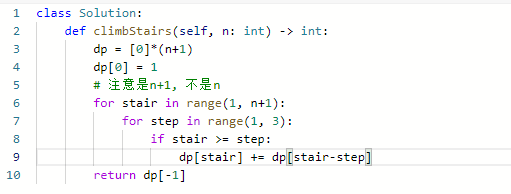
注意和上一道题目一样，需要进行一个判断才写递推式

322. Coin Change

难度中等1844

You are given an integer array coins representing coins of different denominations and an integer amount representing a total amount of money.

Return the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return -1.

You may assume that you have an infinite number of each kind of coin.

Example 1:

Input: coins = [1,2,5], amount = 11
Output: 3
Explanation: 11 = 5 + 5 + 1

Example 2:

Input: coins = [2], amount = 3
Output: -1

Example 3:

Input: coins = [1], amount = 0
Output: 0

思路：

dp数组的意义：dp[j]表示amount为j时，最少的钱币数目
递推式：如果采用coins[i]，dp[j] = dp[j-coins[i]]+1
- 所以dp[j] = min(dp[j-coins[i]]+1, dp[j])
初始化：dp[0] = 0，因为是求最小，所以其他的都给一个较大值amount
确定遍历顺序：因为这道题是求钱币的最小数，所以钱币是有序的或者无序的都行

代码：

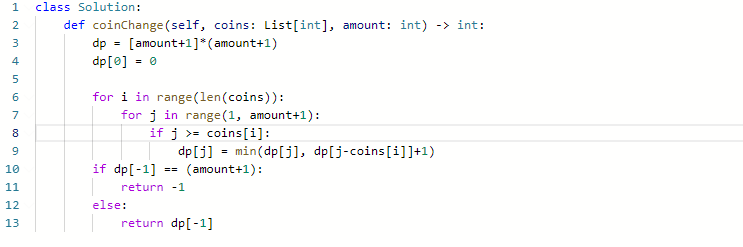
注意要有判断j和coins[i]，并且是大于等于，不是大于

279. Perfect Squares

难度中等1305

Given an integer n, return the least number of perfect square numbers that sum to n.

A perfect square is an integer that is the square of an integer; in other words, it is the product of some integer with itself. For example, 1, 4, 9, and 16 are perfect squares while 3 and 11 are not.

Example 1:

Input: n = 12
Output: 3
Explanation: 12 = 4 + 4 + 4.

Example 2:

Input: n = 13
Output: 2
Explanation: 13 = 4 + 9.

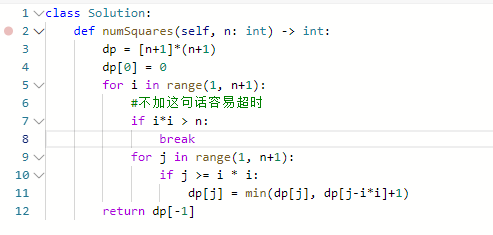
思路：

dp的意义：dp[j]代表j需要最少几个完全平方数
递推式：如果使用了数字i，那么dp[j] = dp[j-i*i]+1
- 所以dp[j] = min(dp[j]+dp[j-i*i+1])
初始化：dp[0] = 0，其他的用n+1
遍历顺序：对于求组合数，外层是遍历物品，内存遍历背包容量；对于求排列数，外层是遍历背包容量，内层是遍历物品。而对于这题，是求最小值，那么就和上一题一样，都是可以的。
举例：

代码：

139. Word Break

难度中等1518

Given a string s and a dictionary of strings wordDict, return true if s can be segmented into a space-separated sequence of one or more dictionary words.

Note that the same word in the dictionary may be reused multiple times in the segmentation.

Example 1:

Input: s = "leetcode", wordDict = ["leet","code"]
Output: true
Explanation: Return true because "leetcode" can be segmented as "leet code".

Example 2:

Input: s = "applepenapple", wordDict = ["apple","pen"]
Output: true
Explanation: Return true because "applepenapple" can be segmented as "apple pen apple".
Note that you are allowed to reuse a dictionary word.

Example 3:

Input: s = "catsandog", wordDict = ["cats","dog","sand","and","cat"]
Output: false

思路：

dp的意义：dp[j]代表对于长度为i的s，到j为止，可不可以被拆分
递推式：如果这个从j-len(word)到j，这些确实是word。那么我们需要考虑的就是dp[j-len(word)]的情况
- dp[j] = dp[j] or (dp[j-len(word)] and word
初始化
- dp[0]必须是True，否则推导存在问题，其余全部是False
遍历顺序
- ~~本题是是否出现过，所以内外循环是遍历那个都可以~~
- 但是实际上我把i和j顺序颠倒就报错了，
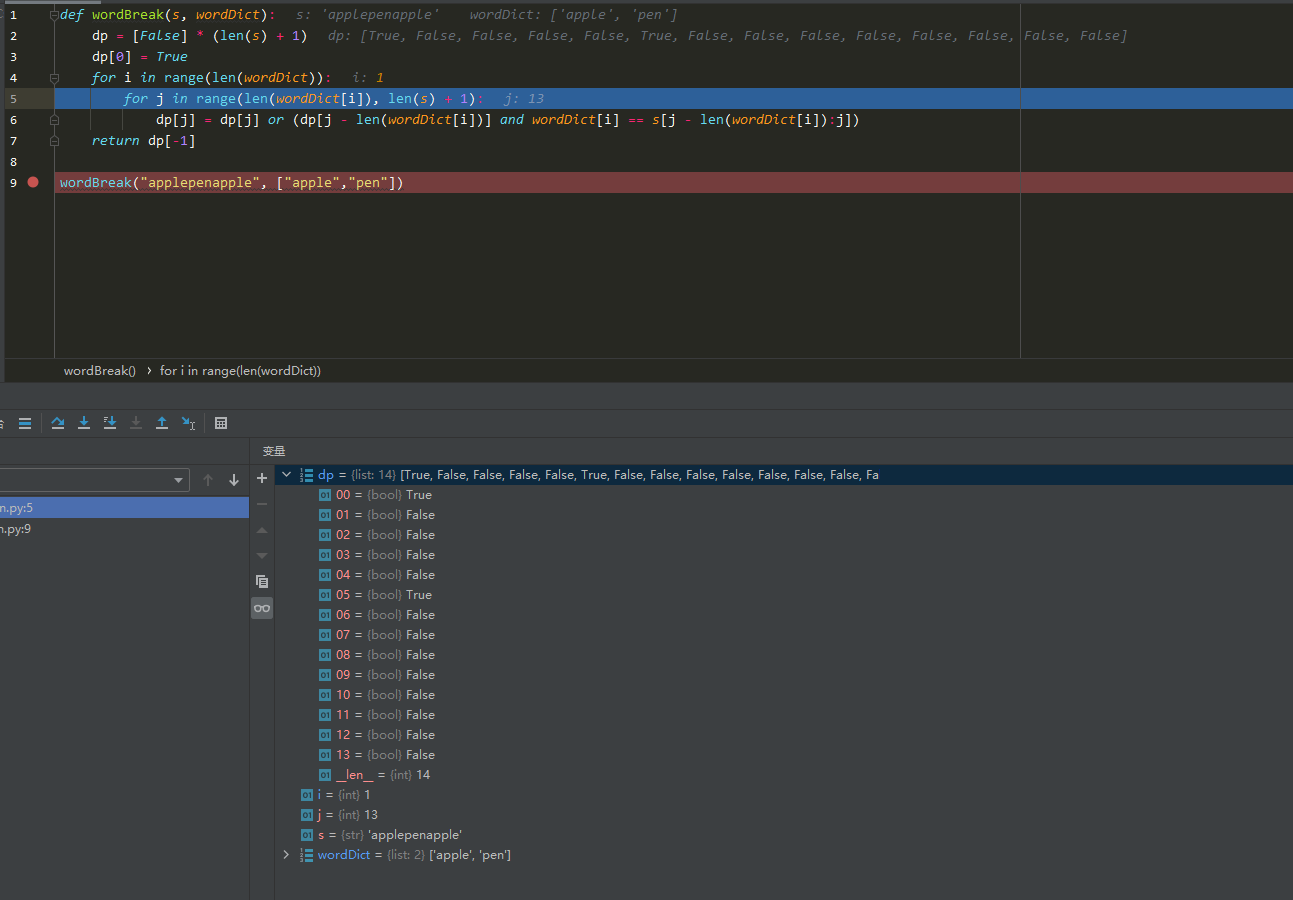
- j=13的时候apple没发现，所以必须外层是背包容量，内层是物品

代码：

时间复杂度是O(n^2), 空间复杂度是O(n)

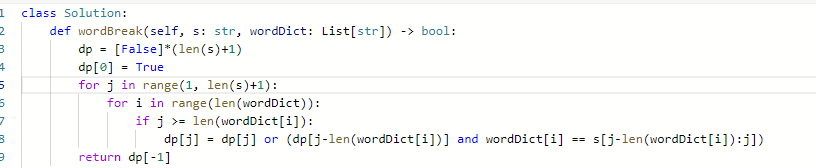
此外，内层是背包的话，一般会出现初始的不同

2.3 背包总结

3. 打家劫舍

198. House Robber

难度中等2034

You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed, the only constraint stopping you from robbing each of them is that adjacent houses have security systems connected and it will automatically contact the police if two adjacent houses were broken into on the same night.

Given an integer array nums representing the amount of money of each house, return the maximum amount of money you can rob tonight without alerting the police.

Example 1:

Input: nums = [1,2,3,1]
Output: 4
Explanation: Rob house 1 (money = 1) and then rob house 3 (money = 3).
Total amount you can rob = 1 + 3 = 4.

Example 2:

Input: nums = [2,7,9,3,1]
Output: 12
Explanation: Rob house 1 (money = 2), rob house 3 (money = 9) and rob house 5 (money = 1).
Total amount you can rob = 2 + 9 + 1 = 12.

思路：

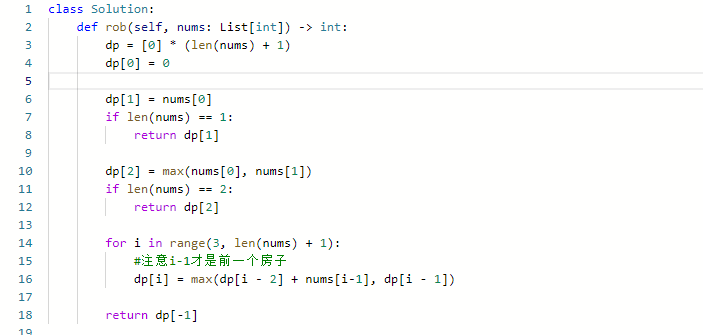
dp的意义：对于前i间房子，我能偷多少钱
递推式：对于dp[j]，如果我偷了j，那么我就不能偷j-1；dp[j] = dp[j-2]+nums[j-1]; 如果没偷j，dp[j] = dp[j-1]
- 所以dp[j] = max( dp[j-2]+nums[j-1], dp[j-1])
- 注意上面nums是j-1，要是觉得不爽，就给nums前面再给一位，或者都用少一位
- 可以感觉到不是要装满的背包问题还是挺不一样的
初始化：dp[0] = nums[0]; dp[1] = max(nums[0], nums[1])
迭代顺序：正序

代码：

213. House Robber II

难度中等988

You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed. All houses at this place are arranged in a circle. That means the first house is the neighbor of the last one. Meanwhile, adjacent houses have a security system connected, and it will automatically contact the police if two adjacent houses were broken into on the same night.

Given an integer array nums representing the amount of money of each house, return the maximum amount of money you can rob tonight without alerting the police.

Example 1:

Input: nums = [2,3,2]
Output: 3
Explanation: You cannot rob house 1 (money = 2) and then rob house 3 (money = 2), because they are adjacent houses.

Example 2:

Input: nums = [1,2,3,1]
Output: 4
Explanation: Rob house 1 (money = 1) and then rob house 3 (money = 3).
Total amount you can rob = 1 + 3 = 4.

Example 3:

Input: nums = [1,2,3]
Output: 3

思路：

dp的意义：还是前j间房子，最多偷dp[j]
递推式：q其实仔细想一下，只有最后那个和第一个之间会存在影响，那么我们可以就计算两次，一次一定不拿第一个，一次一定不拿最后一个。
- 分别构建另外两个list，对于这两个list，使用上一题的策略dp[j] = max( dp[j-2]+nums[j-1], dp[j-1])
- dp[j] = max(dp_0, dp_1)

代码：

337. House Robber III

难度中等1222

The thief has found himself a new place for his thievery again. There is only one entrance to this area, called root.

Besides the root, each house has one and only one parent house. After a tour, the smart thief realized that all houses in this place form a binary tree. It will automatically contact the police if two directly-linked houses were broken into on the same night.

Given the root of the binary tree, return the maximum amount of money the thief can rob without alerting the police.

Example 1:

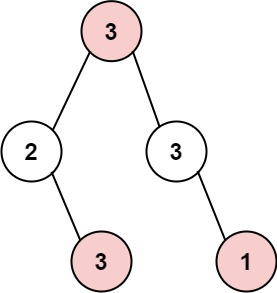
Input: root = [3,2,3,null,3,null,1]
Output: 7
Explanation: Maximum amount of money the thief can rob = 3 + 3 + 1 = 7.

Example 2:

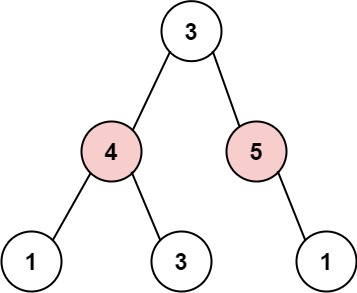
Input: root = [3,4,5,1,3,null,1]
Output: 9
Explanation: Maximum amount of money the thief can rob = 4 + 5 = 9.

思路：

这题和前两个一样，难点仅在于对于树的遍历
对于树的话，首先就要想到遍历方式，前中后序（深度优先搜索）还是层序遍历（广度优先搜索）。

本题一定是要后序遍历，因为通过递归函数的返回值来做下一步计算。
确定遍历顺序：
- 通过递归左节点，得到左节点偷与不偷的金钱；通过递归右节点，得到右节点偷与不偷的金钱。

代码：

4. 股票问题

121. Best Time to Buy and Sell Stock

难度简单2250

You are given an array prices where prices[i] is the price of a given stock on the ith day.

You want to maximize your profit by choosing a single day to buy one stock and choosing a different day in the future to sell that stock.

Return the maximum profit you can achieve from this transaction. If you cannot achieve any profit, return 0.

Example 1:

Input: prices = [7,1,5,3,6,4]
Output: 5
Explanation: Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
Note that buying on day 2 and selling on day 1 is not allowed because you must buy before you sell.

Example 2:

Input: prices = [7,6,4,3,1]
Output: 0
Explanation: In this case, no transactions are done and the max profit = 0.

思路：

毫无疑问，最简单的就是使用贪心算法

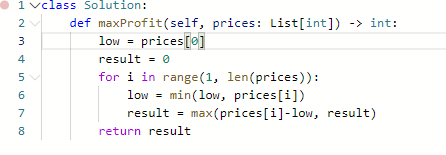
如果使用动态规划，这里需要构建二维的dp

dp数组的意义
- dp[i] [0]代表第i天前买入股票所需要花费的最少金额
- dp[i] [1]代表第i天前出售股票所能获得的最大收益
递推式
- 对于dp[i] [0]
  - 如果第i-1天还没买入，那么必须第i天买了，dp[i] [0] = prices[i]
  - 如果之前买了，dp[i] [0] = dp[i-1] [0]
  - 所以dp[i] [0] = min(dp[i-1] [0], prices[i])
- 对于dp[i] [1];
  - 如果第i-1天已经处于卖出股票的状态，dp[i] [1] = dp[i-1] [1]
  - 如果第i-1天还没卖，第i天卖了，dp[i] [1] = prices[i] - dp[i-1] [0]
  - 所以dp[i] [1] = max(dp[i-1] [1], prices[i] - dp[i-1] [0] )
初始化
- dp[0] [0] =prices[0]
- dp[0] [1] = 0

代码：

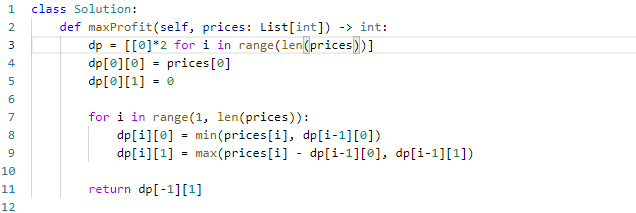
这个复杂度特别高

122. Best Time to Buy and Sell Stock II

难度中等1636收藏分享切换为中文接收动态反馈

You are given an integer array prices where prices[i] is the price of a given stock on the ith day.

On each day, you may decide to buy and/or sell the stock. You can only hold at most one share of the stock at any time. However, you can buy it then immediately sell it on the same day.

Find and return the maximum profit you can achieve.

Example 1:

Input: prices = [7,1,5,3,6,4]
Output: 7
Explanation: Buy on day 2 (price = 1) and sell on day 3 (price = 5), profit = 5-1 = 4.
Then buy on day 4 (price = 3) and sell on day 5 (price = 6), profit = 6-3 = 3.
Total profit is 4 + 3 = 7.

Example 2:

Input: prices = [1,2,3,4,5]
Output: 4
Explanation: Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.
Total profit is 4.

Example 3:

Input: prices = [7,6,4,3,1]
Output: 0
Explanation: There is no way to make a positive profit, so we never buy the stock to achieve the maximum profit of 0.

思路：

这题和上一题唯一的区别就在于递推式
对于dp[i] [0], 也就是在第i天前买入股票所需要花费的最少金额
- 如果第i-1天还没买入，不同于之前必须第i天买，现在可以在第i-1天及之前卖出，所以考虑到最少金额，一定是希望第i-1天前卖出的越高越好：dp[i] [0] 不再是 prices[i]，而应该是prices[i] - dp[i-1] [1]
- 如果第i-1天刚买了，dp[i] [0] = dp[i-1] [0]
- 所以dp[i] [0] = min(dp[i-1] [0], prices[i]- dp[i-1] [1])
对于dp[i] [1];第i天前出售股票所能获得的最大收益
- 如果第i-1天已经处于卖出股票的状态，dp[i] [1] = dp[i-1] [1]
- 如果第i-1天还没卖，第i天卖了，dp[i] [1] = prices[i] - dp[i-1] [0]
- 所以dp[i] [1] = max(dp[i-1] [1], prices[i] - dp[i-1] [0] )
初始化：dp[0] [0] = prices[0]; dp[0] [1]=0

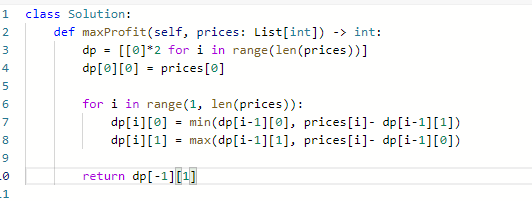
理论上时间复杂度和空间复杂度都是O(n)

另一种思路是可以理解为每天都在买卖

代码：

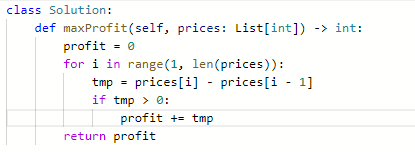
123. Best Time to Buy and Sell Stock III

难度困难1075收藏分享切换为中文接收动态反馈

You are given an array prices where prices[i] is the price of a given stock on the ith day.

Find the maximum profit you can achieve. You may complete at most two transactions.

Note: You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).

Example 1:

Input: prices = [3,3,5,0,0,3,1,4]
Output: 6
Explanation: Buy on day 4 (price = 0) and sell on day 6 (price = 3), profit = 3-0 = 3.
Then buy on day 7 (price = 1) and sell on day 8 (price = 4), profit = 4-1 = 3.

Example 2:

Input: prices = [1,2,3,4,5]
Output: 4
Explanation: Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.
Note that you cannot buy on day 1, buy on day 2 and sell them later, as you are engaging multiple transactions at the same time. You must sell before buying again.

Example 3:

Input: prices = [7,6,4,3,1]
Output: 0
Explanation: In this case, no transaction is done, i.e. max profit = 0.

思路：

从这道题的思路，我们可以看到，有几种状态，dp就需要有几列，121和122就是两列
dp数组和下标的意义：
- dp[i] [j]代表第i天执行j操作
- j=0，不操作
- j=1, 第i天前，第一次买入需要花费的最少钱; 这里不能用贪心策略，因为仅有两次。
- j=2，第一次卖出的收入收入
- j=3, 第二次买入
- j=4，第二次卖出
- 这五个状态依次依赖来更新，如果前一个值为0，比如根本没有进行一次卖出，将也不存在二次买入
递推式：
- 对于dp[i] [1], 之前一定没买过。如果第i天买入，dp[i] [1]= prices[i] - dp[i-1] [0]; 如果第i天不操作，且之前买过，dp[i] [1] = dp[i-1] [1]。所以dp[i] [1] = min( prices[i] - dp[i-1] [0]， dp[i-1] [1])
- 对于dp[i] [2]。如果第i天卖出，dp[i] [2] = prices[i] - dp[i-1] [1]; 如果第i天不操作，dp[i] [2] = dp[i-1] [2]。所以dp[i] [2] = max(prices[i] - dp[i-1] [1], dp[i-1] [2])
- 对于dp[i] [3] = min(prices[i] - dp[i-1] [2], dp[i-1] [3])
- 对于dp[i] [4] = max(prices[i] - dp[i-1] [3], dp[i-1] [4])
初始化：
- 没操作就是0，dp[0] [0] = 0
- 第一次买入肯定是第一天， dp[0] [1] = prices[0]
- 同理dp[0] [2] = 0; dp[0] [4] =0
- dp[0] [3] =prices[0]

代码：

188. Best Time to Buy and Sell Stock IV

难度困难695收藏分享切换为中文接收动态反馈

You are given an integer array prices where prices[i] is the price of a given stock on the ith day, and an integer k.

Find the maximum profit you can achieve. You may complete at most k transactions.

Note: You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).

Example 1:

Input: k = 2, prices = [2,4,1]
Output: 2
Explanation: Buy on day 1 (price = 2) and sell on day 2 (price = 4), profit = 4-2 = 2.

Example 2:

Input: k = 2, prices = [3,2,6,5,0,3]
Output: 7
Explanation: Buy on day 2 (price = 2) and sell on day 3 (price = 6), profit = 6-2 = 4. Then buy on day 5 (price = 0) and sell on day 6 (price = 3), profit = 3-0 = 3.

思路：

和上一题相比，这次允许多次交易了，很显然我们需要的列数是2k+1
递推式和之前一样，初始化是只要是奇数，意味着买入都是初始化为prices[0]

代码：

309. Best Time to Buy and Sell Stock with Cooldown

难度中等1150收藏分享切换为中文接收动态反馈

You are given an array prices where prices[i] is the price of a given stock on the ith day.

Find the maximum profit you can achieve. You may complete as many transactions as you like (i.e., buy one and sell one share of the stock multiple times) with the following restrictions:

After you sell your stock, you cannot buy stock on the next day (i.e., cooldown one day).

Note: You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).

Example 1:

Input: prices = [1,2,3,0,2]
Output: 3
Explanation: transactions = [buy, sell, cooldown, buy, sell]

Example 2:

Input: prices = [1]
Output: 0

思路：

状态一：第i天前买入股票，所需最低金额
状态二：第i天卖出了股票，所获最大收益
状态三：今天为冷冻期
确定递推式：
- 对于状态一，dp[i] [0];
  - 如果之前买入了股票，dp[i] [0] = dp[i-1] [0]
  - 如果今天买入的股票。如果今天刚好是经历了状态三，过了冷冻期，那买入的金额是price[i] - dp[i-1] [2]
  - dp[i] [0] = min( dp[i-1] [0], price[i] - dp[i-1] [2])
- 对于状态二，dp[i] [1];
  - 如果之前卖出了股票，dp[i] [1] = dp[i-1] [1]
  - 如果就是今天卖出的股票，那就是i-1天之前买入的 dp[i] [1] = price[i] - dp[i-1] [0]
  - dp[i] [1] = max(dp[i-1] [1], price[i] - dp[i-1] [0])
- 对于状态三，dp[i] [2];
  - 那么前一天一定是卖出的状态，dp[i] [2] = dp[i-1] [1]
初始化dp[i] [0] =prices[0]

代码：

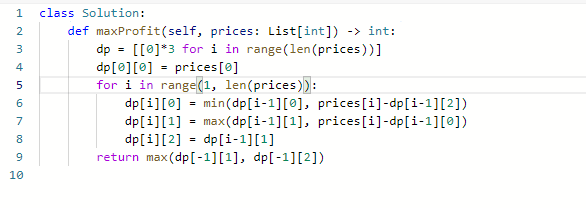
这是我自己的想法，就是要注意for的要从1开始，之后可以看下网上的思路

714. Best Time to Buy and Sell Stock with Transaction Fee

难度中等672收藏分享切换为中文接收动态反馈

You are given an array prices where prices[i] is the price of a given stock on the ith day, and an integer fee representing a transaction fee.

Find the maximum profit you can achieve. You may complete as many transactions as you like, but you need to pay the transaction fee for each transaction.

Note: You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).

Example 1:

Input: prices = [1,3,2,8,4,9], fee = 2
Output: 8
Explanation: The maximum profit can be achieved by:
- Buying at prices[0] = 1
- Selling at prices[3] = 8
- Buying at prices[4] = 4
- Selling at prices[5] = 9
The total profit is ((8 - 1) - 2) + ((9 - 4) - 2) = 8.

Example 2:

Input: prices = [1,3,7,5,10,3], fee = 3
Output: 6

思路：

总体上其实和之前的122相似，可以多次交易，不同的地方在于这次有手续费
所以相似地，也可以使用贪心算法
dp[i] [0] 代表第i天及之前买入股票的最小支出
- 如果第i天之前就买入了dp[i] [0] = dp[i-1] [0]
- 如果恰好是第i天买，dp[i] [0] = price[i] - dp[i-1] [1]
- dp[i] [0] = min(dp[i-1] [0], prices[i] - dp[i-1] [1])
dp[i] [1] 代表第i天及之前卖出股票的最大收入
- 如果第i天之前就卖出了dp[i] [1] = dp[i-1] [1]
- 如果恰好第i天卖，dp[i] [1] = prices[i] - dp[i-1] [0] - fee
- dp[i] [1] = max(dp[i-1] [1], prices[i] - dp[i-1] [0] - fee)
初始化
- dp[0] [0] = prices[0]

代码

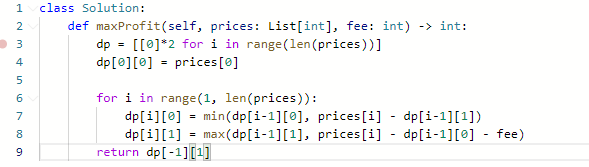
感觉贪心也很简单

5. 子序列问题

300. Longest Increasing Subsequence

难度中等2387

Given an integer array nums, return the length of the longest strictly increasing subsequence.

A subsequence is a sequence that can be derived from an array by deleting some or no elements without changing the order of the remaining elements. For example, [3,6,2,7] is a subsequence of the array [0,3,1,6,2,2,7].

Example 1:

Input: nums = [10,9,2,5,3,7,101,18]
Output: 4
Explanation: The longest increasing subsequence is [2,3,7,101], therefore the length is 4.

Example 2:

Input: nums = [0,1,0,3,2,3]
Output: 4

Example 3:

Input: nums = [7,7,7,7,7,7,7]
Output: 1

思路

dp[j] 代表j之前的最长上升子序列长度, 也就是从0到j-1的比nums[j]小的数字的个数+1,因为自己也要被算上
对于i从0到j-1, 如果nums[i]<nums[j]，那么dp[j] = max(dp[j], dp[i]+1)
使用贪心和二分可以从O(n^2)变到O(nlgn), 二刷的时候看看

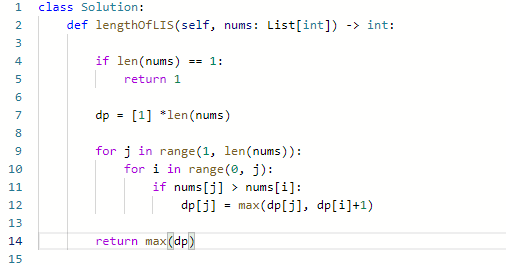
代码：

首先别忘了第十一行的判断
其次是别忘了最后是要返回整个dp中的最大值，不像之前的问题只要最后一个

674. Longest Continuous Increasing Subsequence

难度简单262

Given an unsorted array of integers nums, return the length of the longest continuous increasing subsequence (i.e. subarray). The subsequence must be strictly increasing.

A continuous increasing subsequence is defined by two indices l and r (l < r) such that it is [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] and for each l <= i < r, nums[i] < nums[i + 1].

Example 1:

Input: nums = [1,3,5,4,7]
Output: 3
Explanation: The longest continuous increasing subsequence is [1,3,5] with length 3.
Even though [1,3,5,7] is an increasing subsequence, it is not continuous as elements 5 and 7 are separated by element
4.

Example 2:

Input: nums = [2,2,2,2,2]
Output: 1
Explanation: The longest continuous increasing subsequence is [2] with length 1. Note that it must be strictly
increasing.

思路：

dp[j]表示j之前的最长连续递增子序列的长度,且必须以j结尾！
- 如果不加上以j结尾这个限制，将会很难推导
if nums[j] > nums[j-1], 那么dp[j] = dp[j-1] +1
初始化dp[j]=1

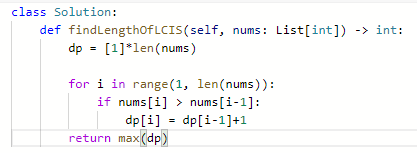
代码：

718. Maximum Length of Repeated Subarray

难度中等659

Given two integer arrays nums1 and nums2, return the maximum length of a subarray that appears in both arrays.

Example 1:

Input: nums1 = [1,2,3,2,1], nums2 = [3,2,1,4,7]
Output: 3
Explanation: The repeated subarray with maximum length is [3,2,1].

Example 2:

Input: nums1 = [0,0,0,0,0], nums2 = [0,0,0,0,0]
Output: 5

思路：

dp[i] [j]代表到nums1的第i个为止和到nums2的第j个为止，最长重复子数组的长度
- 必须说明，是不包含i和j
- 也就是最多到i-1和j-1的重复
- 但是我们的dp会有多给一格，所以最后也能考虑到最后一位
其中如果nums1[i] == nums2[j],那么递推式为dp[i] [j] = dp[i-1] [j-1]+1

代码:

1143. Longest Common Subsequence

难度中等921

Given two strings text1 and text2, return the length of their longest common subsequence. If there is no common subsequence, return 0.

A subsequence of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.

For example, "ace" is a subsequence of "abcde".

A common subsequence of two strings is a subsequence that is common to both strings.

Example 1:

Input: text1 = "abcde", text2 = "ace" 
Output: 3  
Explanation: The longest common subsequence is "ace" and its length is 3.

Example 2:

Input: text1 = "abc", text2 = "abc"
Output: 3
Explanation: The longest common subsequence is "abc" and its length is 3.

Example 3:

Input: text1 = "abc", text2 = "def"
Output: 0
Explanation: There is no such common subsequence, so the result is 0.

思路：

要注意subarray和subsequence的区别，前者要求连续，后者不需要
又是一个两个东西比较的，很自然会想到用一个list table
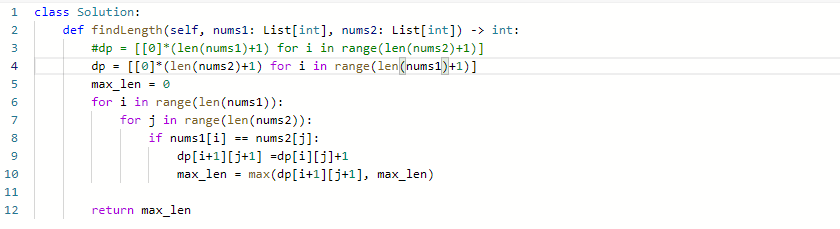
dp[i] [j]代表text1在索引i之前和text2在索引j之前的最长公共subsequence
很显然根据上一题的经验，建立dp时要多一格来确保看到最后一个索引位
如果text1[i-1] == text2[j-1], 那么dp[i] [j] = dp[i-1] [j-1]+1
如果text1[i-1] != text2[j-1], 那么我们就要看
- text1[i-2]和text2[j-1]的最长公共subsequence
- text1[i-1]和text2[j-2]的最长公共subsequence
- dp[i] [j] = max(dp[i-1] [j], dp[i] [j-1])
遍历顺序

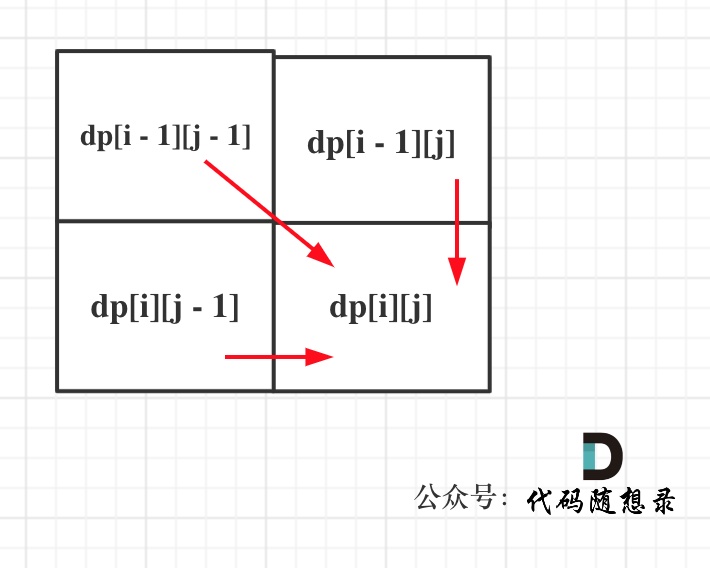
代码：

1035. Uncrossed Lines

难度中等297

You are given two integer arrays nums1 and nums2. We write the integers of nums1 and nums2 (in the order they are given) on two separate horizontal lines.

We may draw connecting lines: a straight line connecting two numbers nums1[i] and nums2[j] such that:

nums1[i] == nums2[j], and
the line we draw does not intersect any other connecting (non-horizontal) line.

Note that a connecting line cannot intersect even at the endpoints (i.e., each number can only belong to one connecting line).

Return the maximum number of connecting lines we can draw in this way.

Example 1:

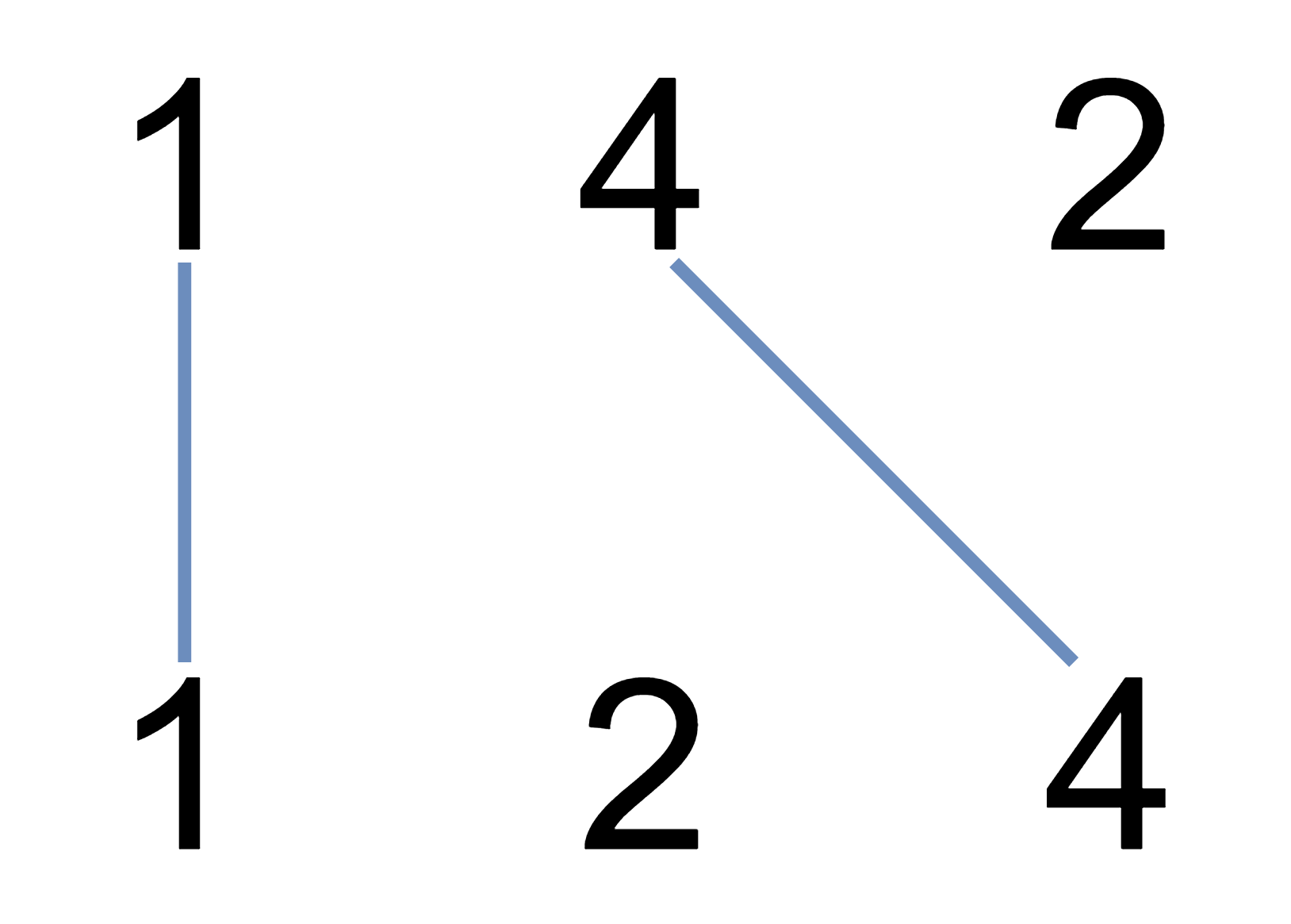
Input: nums1 = [1,4,2], nums2 = [1,2,4]
Output: 2
Explanation: We can draw 2 uncrossed lines as in the diagram.
We cannot draw 3 uncrossed lines, because the line from nums1[1] = 4 to nums2[2] = 4 will intersect the line from nums1[2]=2 to nums2[1]=2.

Example 2:

Input: nums1 = [2,5,1,2,5], nums2 = [10,5,2,1,5,2]
Output: 3

Example 3:

Input: nums1 = [1,3,7,1,7,5], nums2 = [1,9,2,5,1]
Output: 2

思路：

本题说是求绘制的最大连线数，其实就是求两个字符串的最长公共子序列的长度！
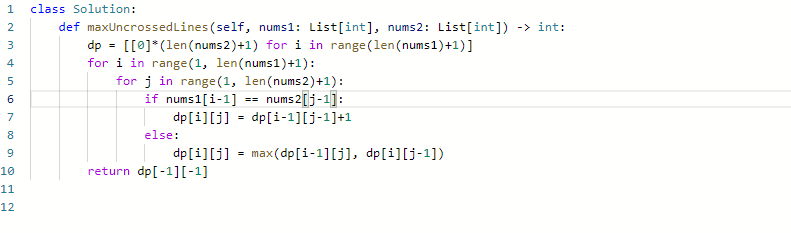
所以你会发现和上一题是完全一样的，甚至代码都不用修改，直接改一下变量名就ok了
直线不能相交，这就是说明在字符串A中找到一个与字符串B相同的子序列，且这个子序列不能改变相对顺序，只要相对顺序不改变，链接相同数字的直线就不会相交

代码：

53. Maximum Subarray

难度简单4687收藏分享切换为中文接收动态反馈

Given an integer array nums, find the contiguous subarray (containing at least one number) which has the largest sum and return its sum.

A subarray is a contiguous part of an array.

Example 1:

Input: nums = [-2,1,-3,4,-1,2,1,-5,4]
Output: 6
Explanation: [4,-1,2,1] has the largest sum = 6.

Example 2:

Input: nums = [1]
Output: 1

Example 3:

Input: nums = [5,4,-1,7,8]
Output: 23

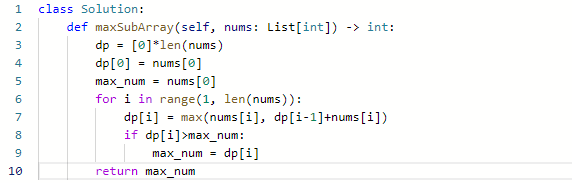
思路:

这题很显然可以使用贪心
如果dp[i] 表示以i结尾的最大连续子序和，这样就是在整个dp遍历过程中找到
- 注意不能到i为止，那样说输出最后一个dp[i]
- 可能这就是连续子序的问题
如果没有包含nums[i]，dp[i] = dp[i-1]
如果包含nums[i], dp[i] = max(dp[i-1]+nums[i], nums[i])
所以，dp[i] = max()

代码：

392. Is Subsequence

难度简单625收藏分享切换为中文接收动态反馈

Given two strings s and t, return true if s is a subsequence of t, or false otherwise.

A subsequence of a string is a new string that is formed from the original string by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (i.e., "ace" is a subsequence of "abcde" while "aec" is not).

Example 1:

Input: s = "abc", t = "ahbgdc"
Output: true

Example 2:

Input: s = "axc", t = "ahbgdc"
Output: false

Constraints:

0 <= s.length <= 100
0 <= t.length <= 104
s and t consist only of lowercase English letters.

Follow up: Suppose there are lots of incoming s, say s1, s2, ..., sk where k >= 109, and you want to check one by one to see if t has its subsequence. In this scenario, how would you change your code?

思路：

这道题看到第一反应就是双指针，但是我们这次要用动态规划
然后又是两个字符串的，很自然就能想到要dp矩阵
dp[i] [j]代表到s[i]和t[j]为止，以下标i-1为结尾和以下标j-1结尾的重复字串长度，如果这个长度恰好等于短的字符串的长度，那么就是True
递推式：
- 如果s[i-1] == t[j-1], 那么dp[i] [j] = dp[i-1] [j-1]+1
- 如果是s[i-1] != t[j-1], 那么他有两个方向的递推
  - dp[i-1] [j]和dp[i] [j-1]

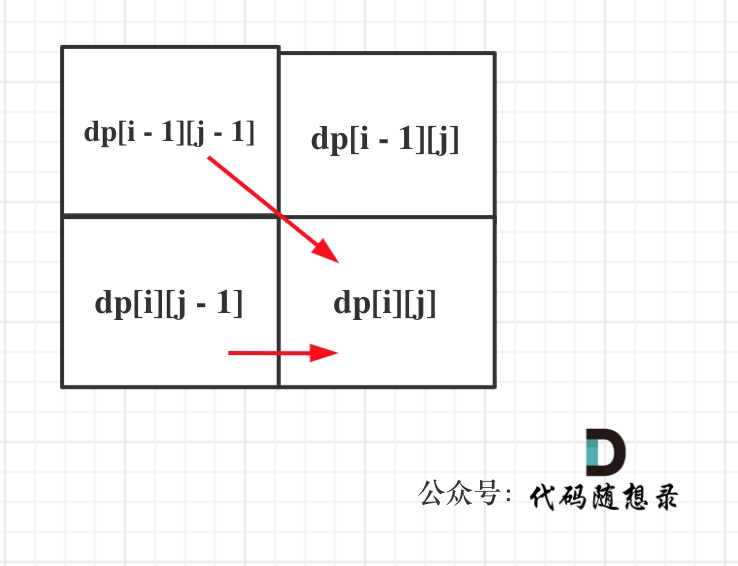
代码:

115. 不同的子序列

难度困难724收藏分享切换为英文接收动态反馈

给定一个字符串 s 和一个字符串 t ，计算在 s 的子序列中 t 出现的个数。

字符串的一个 子序列 是指，通过删除一些（也可以不删除）字符且不干扰剩余字符相对位置所组成的新字符串。（例如，"ACE" 是 "ABCDE" 的一个子序列，而 "AEC" 不是）

题目数据保证答案符合 32 位带符号整数范围。

示例 1：

输入：s = "rabbbit", t = "rabbit"
输出：3
解释：
如下图所示, 有 3 种可以从 s 中得到 "rabbit" 的方案。
rabbbit
rabbbit
rabbbit

示例 2：

输入：s = "babgbag", t = "bag"
输出：5
解释：
如下图所示, 有 5 种可以从 s 中得到 "bag" 的方案。 
babgbag
babgbag
babgbag
babgbag
babgbag

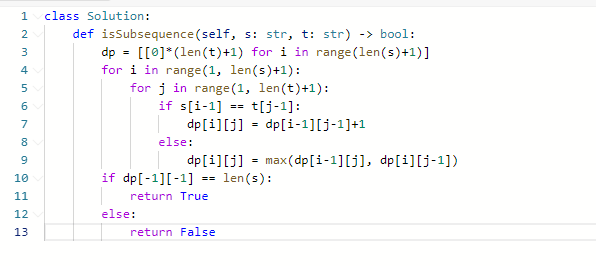
思路：

如果不是子序列，而是要求连续序列的，==那就可以考虑用KMP==。为什么？

这道题目相对于72. 编辑距离，简单了不少，因为本题相当于只有删除操作，不用考虑替换增加之类的
我们知道t是不可分割的，s是可以进行删减的，
所以定义dp[i] [j]为在s[0, i-1]中t[0, j-1]所出现的个数
递推式：
- 如果末尾项不一样（s[i] != t[j]）
- s[i-1] 不能和 t[j-1] 匹配，因此只考虑 t[j-1] 作为 s[i-2] 的子序列，子序列个数为 dp[i-1] [j]
- 如果末尾项一样(s[i]== t[j])，dp[i] [j]的来源有两部份
  - 那么我们可以用s[i-1]和t[j-1] 进行匹配，考虑 t[j-1] 作为 s[i-1] 的子序列，当前的子序列数为dp[i-1] [j-1]
  - 如果我们不用s[i-1]来匹配，考虑 t[j-1] 作为 s[i-2] 的子序列，那么子序列数位dp[i-1] [j]
初始化：
- dp[i] [0] 表示：以i-1为结尾的s删除元素，出现空字符串的个数，有几种方案。显然是1，必须全删，只有这一个方案。
- 再来看dp[0] [j] ：空字符串s删除元素，出现以j-1为结尾的字符串t的个数。显然是0
- dp[0] [0]应该是1，空字符串s，可以删除0个元素，变成空字符串t

代码：

583. 两个字符串的删除操作

难度中等397

给定两个单词 word1 和 word2 ，返回使得 word1 和 word2 相同所需的最小步数。

每步可以删除任意一个字符串中的一个字符。

示例 1：

输入: word1 = "sea", word2 = "eat"
输出: 2
解释: 第一步将 "sea" 变为 "ea" ，第二步将 "eat "变为 "ea"

示例 2:

输入：word1 = "leetcode", word2 = "etco"
输出：4

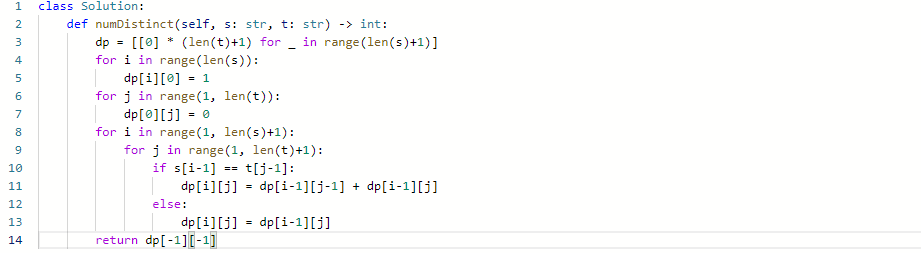
思路：

只要求出两个字符串的最长公共子序列长度即可，那么除了最长公共子序列之外的字符都是必须删除的，最后用两个字符串的总长度减去两个最长公共子序列的长度就是删除的最少步数。
参考1143

代码：

72. 编辑距离

难度困难2275收藏分享切换为英文接收动态反馈

给你两个单词 word1 和 word2， 请返回将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

插入一个字符
删除一个字符
替换一个字符

示例 1：

输入：word1 = "horse", word2 = "ros"
输出：3
解释：
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')

示例 2：

输入：word1 = "intention", word2 = "execution"
输出：5
解释：
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')

思路：

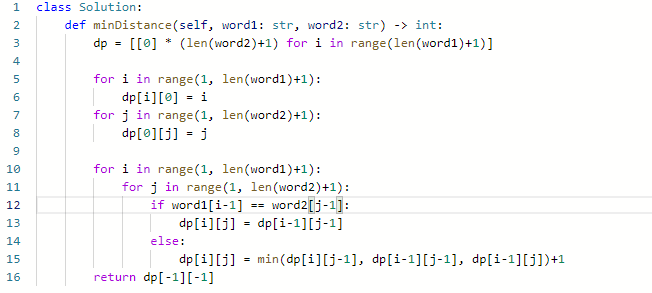
dp[i] [j] 表示以下标i-1为结尾的字符串word1，和以下标j-1为结尾的字符串word2，最近编辑距离为dp[i] [j]
和之前题目一样，从后往前看
对于word1[i-1]和word2[j-1]
- 如果相等，就不操作，相当于抵消，也就是都删除，dp[i] [j] = dp[i-1] [j-1]
- 如果不相等，因为是把word1变成word2，word2是永远不变的，删除word1的东西，dp[i] [j] = dp[i-1] [j] +1
- 如果增加，dp[i] [j] = dp[i] [j-1] +1
- 如果替换，dp[i] [j] = dp[i-1] [j-1] +1
初始化，dp[0] [0]没有意义，设为0，dp[i] [0] = i, 也就是把word1变成空字符串；dp[0] [i] = i, 也就是把空字符串变成word2

代码：

647. 回文子串

难度中等824收藏分享切换为英文接收动态反馈

给你一个字符串 s ，请你统计并返回这个字符串中 回文子串 的数目。

回文字符串 是正着读和倒过来读一样的字符串。

子字符串 是字符串中的由连续字符组成的一个序列。

具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被视作不同的子串。

示例 1：

输入：s = "abc"
输出：3
解释：三个回文子串: "a", "b", "c"

示例 2：

输入：s = "aaa"
输出：6
解释：6个回文子串: "a", "a", "a", "aa", "aa", "aaa"

思路：

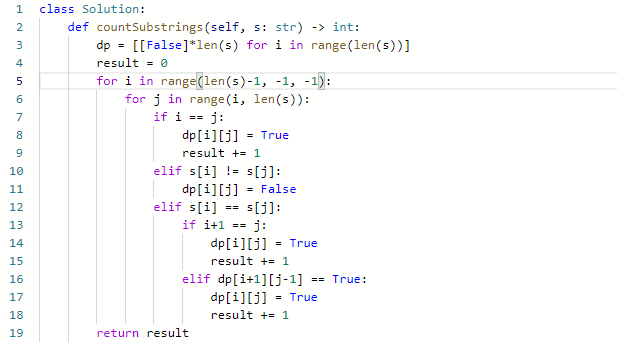
dp[i] [j]代表从下标i到下标j之间是不是回文子串，注意，不是有多少，而是是不是，要不然就错了
对于递推式，如果s[i] != s[j], 那么dp[i] [j] 显然是false，那么如果二者相等：
- 如果i和j下标一样，i=j，s[i] == s[j], dp[i] [j] = True
- 如果i和j下标相差1，s[i] == s[j], dp[i] [j] = True
- 否则就是下标相差1以上，所以就是判断dp[i+1] [j-1]是不是True，如果他是True，那么dp[i] [j]就是true
特别需要注意的是遍历顺序，因为dp[i] [?]需要依赖dp[i+1] [？+1]，所以i一定要是倒序遍历
不要小看遍历顺序的确认！

代码：

516. 最长回文子序列

难度中等767收藏分享切换为英文接收动态反馈

给你一个字符串 s ，找出其中最长的回文子序列，并返回该序列的长度。

子序列定义为：不改变剩余字符顺序的情况下，删除某些字符或者不删除任何字符形成的一个序列。

示例 1：

输入：s = "bbbab"
输出：4
解释：一个可能的最长回文子序列为 "bbbb" 。

示例 2：

输入：s = "cbbd"
输出：2
解释：一个可能的最长回文子序列为 "bb" 。

思路：

上一题中的回文子串是连续的，但是回文子序列不要求连续
定义dp[i] [j] 代表从下标i到下标j的最长回文子序列长度
如果s[i] == s[j], 那么dp[i] [j] = dp[i+1] [j-1]+2
如果s[i] != s[j], 那么dp[i] [j] = max(dp[i+1] [j], dp[i] [j-1])
初始化：dp[i] [i] = 1
遍历顺序：注意i需要依赖i+1来推导出来，所以i是倒序，j是正序

代码：

#注意j一定要比i大！